Basic Statistics with R

Welsch ANOVA

In one way ANOVA, the independent samples are assumed to be drawn from Gaussian distributions whose variances are equal. When this assumption on the equality of the variances across samples is not met, Welsch ANOVA (also called "Welsch F-test") is a better option for testing the equlaity of more than two populations means.

This method still assumes that the data sets whose population means are compared are randomly drwn from Guassians with unequal variances.

Thus the Welsch ANOVA is an alternative to one factor ANOVA when the variances are unequal or sample sizes are small.

In Welch F-test, a weight $w_i$ which is inversely proportional to the variance of sample $i$ is used to reduce the effect of heterogenity across the samples.

If \(s_i\) is the observed variance of sample \(i\), then the weight \(w_i\) for the sample of size $n_i$ is defined as, \(~~w_i = \dfrac{n_i}{s_i^2} \)

The rest of the procedure is very similar to one way ANOVA except for the fact that the weighted means and variances are used instead of normal means and variances.

In the following description, we adopt the same methods and symbols we have used in our derivation of one way anova.

Thus, in Welsch F-test, the grand mean $\overline{X}_{..}$ of the whole data is computed based on the weighted mean for each data set.

If there are m data sets, then the grand mean of the Welsch ANOVA is written as,

$~~~~~~~~~~~~~~\overline{X}_{..}~=~\displaystyle { \dfrac{\sum\limits_{i=1}^m w_i \overline{X}_{i.}}{\sum\limits_{i=1}^{m} w_i}} ~~~~~~~~~$ where $\overline{X}_{i.}$ is the sample mean of the ${\large{i}}^{th}$ group.

In the next step, using the weights, we compute the sum of squares among the treatements (called between the sum of square) as,

$~~~~~~~~~~~~~SSA_{w}~=~\displaystyle \sum\limits_{i=1}^m w_{i}(\overline{X}_{i.} - \overline{X}_{..})^2 $

We denote $ w = \displaystyle \sum\limits_{i=1}^{m} w_{i}$ and introdyce a variable $\lambda$ as,

$~~~~~~~~~~~~~~~{\lambda} = \displaystyle \dfrac{3 \sum\limits_{i=1}^{m} \dfrac{1}{(n_i - 1)} \left(1 - \dfrac{w_i}{w}\right)^2 } {m^2 - 1} $

Using this variable, the Welsch F statistic for the statistical test is defined as,

$~~~~~~~~~~~~~~F_w~=~\displaystyle \dfrac{ {\left(\dfrac{SSA_w}{m-1}\right)} }{1 + \dfrac{2\lambda(m-2)}{3} }~~~{\Large \sim}~~~ F(m-1, \dfrac{1}{\lambda})~~$ is a F variable with $(m-1, \dfrac{1}{\lambda})$ degrees of freedom under the null hypothesis of equality of means.

The null and alternate hypothesis for the Welsch ANOVA are written as,

$~~~~~~~~~~~~~H_0~:~~\mu_1 = \mu_2 = \mu_3 = ...... = \mu_m $

$~~~~~~~~~~~~~H_A~:~~Not~all~the~\mu_i~are~equal$.

Therefore, if $\alpha$ is the significance level for rejecting the test,

We accept the null hypothesis $H_0~$ if $~ F_w \leq F_{1-\alpha}(m-1, \dfrac{1}{\lambda})$

We reject the null hypothesis $H_0$ and accept the alternative if $~ F_w \gt F_{1-\alpha}(m-1, \dfrac{1}{\lambda})$


$~~~~~~~~~~~~~~~~~~~~~~~~~$ Important Note : When the assumptions on the equality of mean are not met, we can use Welsch ANOVA instead of one way ANOVA. However, this method has two limitations:

$~~~~~~$ 1. Welsch ANOVA has fewer degrees of freedom when compared to one way ANOVA since $\dfrac{1}{\lambda} \leq (n + m -1)$, where m is the number of data sets and n is the total number of data points and (n+m-1) is the degrees of freedom used in the one way ANOVA.

Cosequently, Welsch ANOVA is less powerful than the one way ANOVA test.

2. Since the weight factor in the Welsch ANOVA is $w_i = \dfrac{n_i}{s_i^2}$, when the number of obdervations $n_i$ are small, the corresponding weight factor gets smaller making the Welsch ANOVA less reliable than the one way ANOVA for the small sample sizes.

Example-1 :

The cholesterol level of four groups of adults with distince food habits among the groups were compared in an experiment. The results are present below:

$Group-1~:~~220~~214~~203~~184~~186~~200~~165$
$Group-2~:~~262~~193~~225~~200~~164~~266~~179$
$Group-3~:~~272~~192~~190~~208~~231~~235~~141$
$Group-4~:~~190~~255~~247~~278~~230~~269~~289$

Assuming that these four data sets follow Normal distributions $N(\mu_i, \sigma)$, test the null hypothesis that $\mu_1=\mu_2=\mu_3=\mu_4$ to a significance level of 0.05.


We assume that the four populations to be Gaussian with unequal standard deviations and perform Welsch ANOVA to test the equality of their populations means.

For the convenience of symbols, let us denote the four data sets as $X_1, X_2, X_3$ and $X_4$. We write the ANOVA table to perfor the computation as follows:

------------------------------------------------------------------------------------------------------------------------------
$Variable~~~~~~~~~~~~~~~~~~~~~Observations~~~~~~~~~~~~~~~~~~~~~~n_i~~~~~~~\displaystyle\sum_{j=1}^{7}X_{ij}~~~~~~~S_i^2~~~~~~~~~~~~w_i = \dfrac{n_i}{s_i^2}$
------------------------------------------------------------------------------------------------------------------------------
$~~~X_1~~~~~~~~~~~~220~~214~~203~~184~~186~~200~~165~~~~~~~~~7~~~~~~~~1372~~~~~~~~~~~361.66~~~~~~~~~0.019350$

$~~~X_2~~~~~~~~~~~~262~~193~~225~~200~~164~~266~~179~~~~~~~~~~7~~~~~~~~1489~~~~~~~~~~1579.90~~~~~~~0.004430$

$~~~X_3~~~~~~~~~~~~272~~192~~190~~208~~231~~235~~141~~~~~~~~~~7~~~~~~~~1469~~~~~~~~~~1733.14~~~~~~~0.004039$

$~~~X_4~~~~~~~~~~~~190~~255~~247~~278~~230~~269~~289~~~~~~~~~~7~~~~~~~~1758~~~~~~~~~~1115.14~~~~~~~0.006277$

--------------------------------------------------------------------------------------------------------------------------------
$~~~~~~~~~~~~~~~~~~~~Totals~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~28~~~~~~~~~6088~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~0.03410$
--------------------------------------------------------------------------------------------------------------------------------

We now compute the mean $\overline{X}_{i.}$ each group i and the whole mean $\overline{X}_{..}$ as follows:

$~~~\overline{X}_{1.} = \dfrac{1372}{7} = 196.0$, $~~~\overline{X}_{2.} = \dfrac{1489}{7} = 212.7$,

$~~~\overline{X}_{3.} = \dfrac{1469}{7} = 209.85$, $~~~\overline{X}_{4.} = \dfrac{1759}{7} = 251.14$

$\overline{X}_{..}~=~\displaystyle { \dfrac{\sum\limits_{i=1}^m w_i \overline{X}_{i.}}{\sum\limits_{i=1}^{m} w_i}}$
$~~~=~\dfrac{(0.019350 \times 196.0) + ( 0.004430 \times 212.7) + (0.004039 \times 209.8) + (0.006277 \times 251.3)}{0.034096}$
$~~~=~~209.96$

We next compute the Sum of Squares among the treatment:

$SSA_{w}~=~\displaystyle \sum\limits_{i=1}^m w_{i}(\overline{X}_{i.} - \overline{X}_{..})^2 $

$~~~~~~~~~~=~0.019350 \times (196.0 - 209.98)^2 ~+~ 0.004430 \times (212.7 - 209.98)^2$ $~~~~~~~~~~~~~~~~~~~~~~~+~ 0.004039 \times (209.8 - 209.98)^2~+~0.006277 \times (251.3 - 209.98)^2 $

$~~~~~~~~~~=14.4519$

The sum of weights$~~ w = \displaystyle \sum\limits_{i=1}^{m} w_{i}~=~ 0.034096,~~~$ number of groups $~~m = 4$ .

${\lambda} = \displaystyle \dfrac{3 \sum\limits_{i=1}^{m} \dfrac{1}{(n_i - 1)} \left(1 - \dfrac{\omega_i}{\omega}\right)^2 } {m^2 - 1} $

$~~~=~ \dfrac{3}{15} \times \left[ \dfrac{1}{6} \left(1 - \dfrac{0.019350}{0.034096}\right)^2 + \dfrac{1}{6} \left(1 - \dfrac{0.004430}{0.034096}\right)^2 + \dfrac{1}{6} \left(1 - \dfrac{0.004039}{0.034096}\right)^2 \\ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~+ \dfrac{1}{6} \left(1 - \dfrac{0.006277}{0.034096}\right)^2 \right ] $

$~~~~~=~0.07956$

$~~~~~~~~~~~~~~F_w~=~\displaystyle \dfrac{ {\left(\dfrac{SSA_w}{m-1}\right)} }{1 + \dfrac{2\lambda(m-2)}{3} }~=~\displaystyle \dfrac{ {\left(\dfrac{14.4519}{4-1}\right)} }{1 + \dfrac{2 \times 0.07956 \times(4-2)}{3} } ~= 4.3552$

This $F_w$ is a F variable with $(m-1, \dfrac{1}{\lambda})$ degrees of freedom.

Here,$~~~~~~m-1 = 3,~~~\dfrac{1}{\lambda} = \dfrac{1}{0.07956}~=~12.569$

$F_{1 - 0.05}(3,12.569)~=~qf(0.95,3,12.56)~=~3.4437$

The critical region for rejection of null hypothesis is $~~F \ge 3.4437$.

Since the computed value $F=4.3552$ is outside the critical region, we reject the null and accept the alternate hupothesis to conclude that the four population means are not equal.

The p-value for the test is given by area under $F(>4.3552, 3, 12.56) = 1 - pf(4.3552, 3, 12.569) = 0.025766$, which rejects the null at a significance level of 0.05.















































































R scripts 



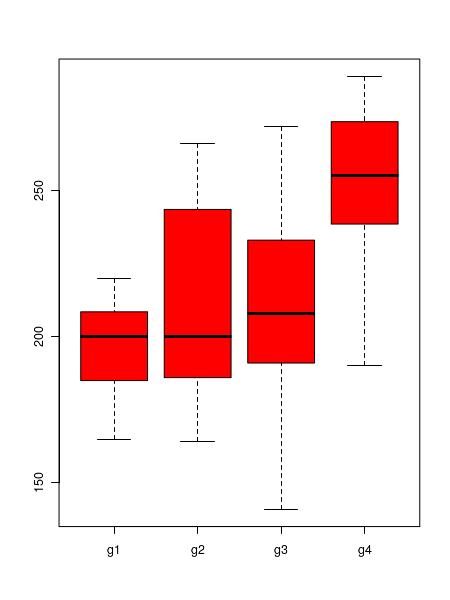
In R, two functions namely aov() and oneway.test()
perform one way anova. They have a very specific inut data structure in the form of a 2 column data frame with category and values of data. 

First step is to create the input file from data. Te second step is to run call the functions in R script.

For example, consider the cholesterol level data among four groups Group-1, Group-2, Group-3 
and Group-4 presented in Example-1. We show it below:

Group−1 :  220  214  203  184  186  200  165
Group−2 :  262  193  225  200  164  266  179
Group−3 :  272  192  190  208  231  235  141
Group−4 :  190  255  247  278  230  269  289

We shorten the names to G1, G2, g3 and G4. 

These 4 setscan be written as a two column data in which first column is the value against 
which the group label is given. See below:

(two colums can be tb separated(*.txt file) or comman separated (*.csv file)

value  group
220     g1
214     g1
203     g1
184     g1
186     g1
200     g1
165     g1
262     g2
193     g2
225     g2
200     g2
164     g2
266     g2
179     g2
272     g3
192     g3
190     g3
208     g3
231     g3
235     g3
141     g3
190     g4
255     g4
247     g4
278     g4
230     g4
269     g4
289     g4

The above data format is stored as a text file with a txt extension. 
We give some name like, "cholesterol_anova_data.txt". 
It can also be stored as a comma separated csv format.

This has the advantage that we can handle data sets of different lengths. 
If you store it as data frame, then many NA's may be required to make them equaal length. 
Above format is better.

Once this file "anova_data.txt" is ready, we can write an R script 
for performing one factor ANOVA as follows:




##analysis of oneway anova in R

## read data into a frame called "dat"
dat = read.table("cholesterol_anova_data.txt", header=TRUE)

## compute and print the mean values of groups
print( mean(dat$value[dat$group=="g1"]) )
print( mean(dat$value[dat$group=="g2"]) )
print( mean(dat$value[dat$group=="g3"]) )
print( mean(dat$value[dat$group=="g4"]) )

## box plot to compare the data sets
boxplot(dat$value ~ dat$group, col="red")

# one way anova test. Default assumption is variances not equal.
oneway.test(dat$value~dat$group, var.equal=FALSE)




(i) In the above script, the call boxplot(dat$value ~ dat$group, col="red") creates the 

following plot:

We can clearly see that there is a substantial difference of means within the four data sets.








(ii) The function call  oneway.test(dat$value~dat$group, var.equal=FALSE)  with the assumption that 

the variances  are unequal (default assumption, Welsch anova) to print the following results:



	One-way analysis of means (not assuming equal variances)

data:  dat$value and dat$group
F = 4.3553, num df = 3.000, denom df = 12.568, p-value = 0.02577


For a F statisti value of 4.355 with 3 degrees of freedom, the p-value for the test is 0.02577. 
If we set an alpha = 0.05, this rejects the null hypothesis that the mean cholesterol 
levels for the 4 groups are equal