Basic Statistics with R

Conditional Probability

There are occasions when we have to compute the probabilities of events under certain conditions . This is called conditional probability.


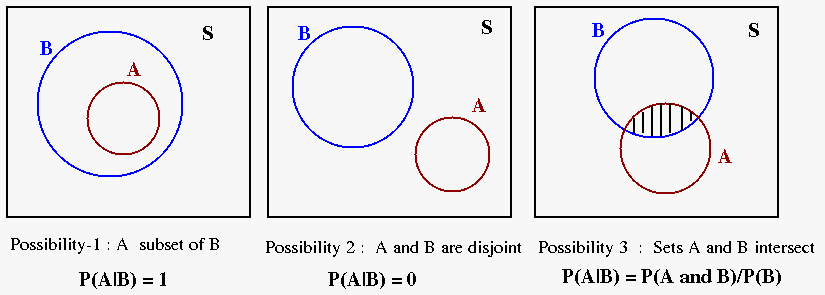
Let S be a set of numbers, of which A and B are subsets.
Given that a randomly chosen number from S is a member of set B, what is the probability that it belongs to set A?


We denote this \(\small{P(A|B)}\) = conditional probability of A given that B has occured


There are three possibilities with A and B. See the diagram below:





Possibility 1 : B is a subset of A. In this case, P(A|B) = 1.

If A consists of even numbers and B consists of numbers that are divisible by 4, then the probability that a selected number that is divisible by 4 to be even is one. ie., P(A|B) = 1


Possibility 2 : A and B are disjoint, without common elements . P(A|B) = 0.

If A consists of odd numbers and B has numbers divisible by 2 as members, then the probability that a randomly picked number from B to be odd is zero. ie., P(A|B) = 0

Possibility 3 : The sample spaces of A and B intersect (ie., they have common elements, indicated by the shaded region in the figure.). This intersection is the region where we can say that A occurs whenever B has occured.


\(\small{ P(A|B) = \dfrac{n(A \cap B)}{n(B)} = \dfrac{p(A \cap B)}{p(B)} }\)


We randomly choose a number between 1 and 20. If it is found to be an odd number, what is the probability that it is divisible by 3?


This problem can be expressed in set theory notation. Consider the set of numbers between 1 to 20 as a sample space S. For our question, let subset B represents the odd numbers between 1 and 20 and subset A represents the number divisible by 3 in the same range 1 to 20. Thus, A and B are subsets of S.


\(S = \{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20\}\)
\(B = \{1,3,5,7,9,11,13,15,17,19\}\)
\(A = \{3,6,9,12,15,18\} \)


Here we try to define the probability of event A(selecting a number divisible by 3), considering only the elements of B(odd numbers between 1 to 20). If we take the elements of B (odd number between 1 to 20), what is the probability of observing event A in it (number divisible by 3)? It is just the fraction of elements of B that are also the members of A.


\(\small{ P(A|B) = \dfrac{n(A \cap B)}{n(B)} = \dfrac{3}{10} }\)



In general, the conditional probability is defined as follows:


Given two events A and B in the same event space with P (B) > 0, the conditional probability of A given B is defined as


\(\small{ P(A|B) = \dfrac{p(A \cap B)}{p(B)} = \dfrac{Joint~probability~of~A~and~B}{Probability~of~B} }\)






By the same logic we see that the conditional probability of B given A is defined as


\(\small{ P(B|A) = \dfrac{p(A \cap B)}{p(A)} = \dfrac{Joint~probability~of~A~and~B}{Probability~of~A} }\)






Important Note : In general, \(\small{ P(B|A) \neq P(A|B)~~~~ }\) (unless A and B have same elements).

Example 1:

In a town affected by a season of epidemics, two diseases D1 and D2 are prevalent. It was estimated that 3.2% of the population contracted the disease D1 and 1.6% of the population has contrated both the diseases. Estimate the probability that a person who is affected by the disease D1 to get the disease D2.

Using the expression for the conditional probability, we have

\( \small{P(D2|D1) = \dfrac{P(D1 \cap D2)}{P(D1)} = \dfrac{0.016}{0.032} = 0.5} \)

Therefore, there is 50% chance that the person who contracted disease D1 will also get the disease D2.



The multiplication rule

From the expressions \(\small{ P(A|B) = \dfrac{P(A \cap B)}{P(B)} }\) and \(\small{ P(B|A) = \dfrac{P(A \cap B)}{P(A)}}\), we can write the expressions for the probability that the events A and B both occur as


\(\small{ P(A \cap B) = P(B|A) P(A) = P(A|B) P(B) }\)


The above relationship is called the multiplication rule .


Example : 40% of the families living in a city posses a two wheeler. 20% of those whos posses two wheeler also own a car. What is the probability that a family owns a car and a two wheeler?

From the data given,

\( \small{P(two~wheeler) = 0.4,~~~~P(car|two~wheeler) = 0.2 }\)

Applying multiplication rule, we have


\(\small{ P(car~and~two~wheeler) = P(car|two~wheeler) P(two~wheeler) = 0.2 \times 0.4 = 0.08 }\)

Therefore, 8% of the families own a car and a two wheeler.



Independent events

Two events are independent if the outcome of the first event does not affect the outcome of the other.


For two independent events A and B,


\(\small{ P(A \cap B) = P(A) \times P(B)} \)



Thus, if two coins are tossed simulataneously, the probability of first one landing with head up and the second one landing with tail up is given by,


\( \small{P(H~and~T) = P(H) \times P(T) = \dfrac{1}{2} \times \dfrac{1}{2} = \dfrac{1}{4} }\)


The above concepts can be extended to independence of any number of events:


\( \small{ P(A \cap B \cap C .....) = P(A) \times P(B) \times P(C) \times ..... }\)


Example : Suppose event A consists of tossing a coin, event B consists of rolling a dice and event C consists of drawing a King randomly from a deck of cards. If these three events are performed simultaneously, what is the probability of getting a head in coin toss, getting a 5 in dice throw and drawing a King randomly from the pack of cards?
We have, \(\small{ ~~~~~~~P(Head) = \dfrac{1}{2},~~~~P(5) = \dfrac{1}{6},~~~and~~~P(king) = \dfrac{4}{52}} \)

Since these three events are independent of each other,


\(\small{ P(Head~and~5~and~King) = P(H) \times P(5) \times P(king) = \dfrac{1}{2} \times \dfrac{1}{6} \times \dfrac{4}{52} = \dfrac{4}{624} } \)



Dependent events

Two events are dependent if the occurance of one affects the probability of occurance of the other. In that case we use the conditional probability to compute the probability of occurance of both simultaneously:


\( \small{P(A \cap B) = P(B|A) P(A) = P(A|B) P(B) }\)





Often we compute the probability of randomly selecting certain objects in succession out of many available objects. While doing so, two situations arise. We can draw objects successively from a collection either with replacement or without replacement.


Successive draws with replacemet makes them independent evets . For example, consider a bag with 5 red marbles and 3 black marbles. Suppose we draw a marble randomly from the bag, note its color and replace it in the bag. The probability of drawing a red marble is \(\small{\frac{5}{8} } \). Now if we draw a marble second time from this bag after replacement, the probabilities of getting a red marble in the second draw is again \(\small{\frac{5}{8} } \), exactly same as the first draw. So, the probability of getting red marble in two successive draws is,


\(\small{P(red~in~first~draw) \times P(black~in~second~draw) = \dfrac{5}{8} \times \dfrac{5}{8} }\)

Suppose, after drawing red marble first time, we do not replace it in the bag. Then, during the second draw, one red marble will be less compared to the first time. This changes the probability of drawing a red marble second time. Now since we have 5 − 1 = 4 red marbles left in the bag, the probaility of selecting a red marble second time is \(\small{\dfrac{4}{7}}\) .
Therefore,


\(\small{ P(red~in~first~draw) = \dfrac{5}{8} }\)
\( \small{P(red~in~second~draw | red~in~first~draw) = \dfrac{4}{7}} \)

Therefore, \(\small{ P(red \cap red) = P(red~in~second~draw | red~in~first~draw) \times P(red~in~first~draw) = \dfrac{4}{7} \times \dfrac{5}{8} }\)


We should remember the basic connection:
successive drawing with replacement ---> independent events
successive drawing without replacement --- > dependent events




Mutually exclusive events

Two or more events are mutually exclusive if the occurance of one of them completely exlcudes the possibility of occurance of all the others. For example, the occurance of Head and Tail in a coin toss are mutually exclusive. The six outcomes 1,2,3,4,5 and 6 of a dice throw are mutually exclusive events.


In general,
\(\small{ P(A \cap B) = P(A) + P(B) - P(A \cup B )}\)

If two events are mutually exclusive, \(\small{P(A \cap B)}\) is not possible. The probability \(\small{P(A \cup B)}\) for any one of them to occur will be equal to the sum of their individual probabilities of occurance.
\(\small{ P(A \cup B) = P(A) + P(B)}\)


We can extend this to any number of mutually exclusive events A,B,C,... to write,


\(\small{ P(A~or~B~or~C ....) = P(A) + P(B) + P(C) + .... }\)
Example :
In a dice throw, compute the probability that the outcome is an odd number.

The outcome can be odd in one of the three mutually exclusive ways : 1, 3, and 5. Therefore,


\(\small{ P(odd~number) = P(1) + P(3) + P(5) = \dfrac{1}{6} + \dfrac{1}{6} + \dfrac{1}{6} = \dfrac{3}{6} }\)