Biostatistics with R

Negative binomial distribution

Suppose we perform a sequence of Bernoulli trials and count the number of successess and failures. If \(\small{p}\) is the probability of success in any trial, how many trials we have to perform until we observe \(\small{r}\) successes?.


Here we are interested in a random variable \(\small{X}\) that represents the number of trials needed to observe the \(\small{r^{th}}\) success. Thus we may observe \(\small{r=5}\) successes in \(\small{X=8}\) trials or in \(\small{X=11}\) trials or in \(\small{X=9}\) trials. X is the trial number in which \(\small{r^{th} }\) success is observed, with \(\small{X \geq r }\). The observed values of the variable X follow the negative binomial distribution .


Another version of the negative binomial distribution is written in terms of the number of failures y before \(\small{r^{th}}\) success.


We will now derive expression for both the probability distribution for both the vairables \(\small{ x}\) and \(\small{ y}\) :



Derivation of the negative binomial probability:

Version 1 : Number of trials \(\small{x}\) needed to observe \(\small{r^{th}}\) success.

\(\small{P_{nb}(x,p,r) = P(x~trials~for~r~successes)}\)

\(~~~~~~~~~~~~~~~~=~P(r-1~successes~in~the~first~x-1~trials) \times P(success~on~r^{th}~trial) \)

We have,

\( \small{P(r-1~successes~in~the~first~x-1~trials)~=~_{x-1}C_{r-1} p^{als~r-1} (1-p)^{x-r}~~~~~(binomial~distribution) }\)

\(\small{P(success~on~r^{th}~trial) = p }\)

We can thus write,

\( P_{nb}(x,p,r) = \small{P(x~trials~for~r~successes)~=~_{x-1}C_{r-1} p^{r-1} (1-p)^{x-r} \times p~=~_{x-1}C_{r-1} p^{r} (1-p)^{x-r} } \)



Version 2 : Number of failures \(\small{y}\) before the \(\small{r^{th}}\) success.


Since \(\small{x }\) is the total number of trials before \(\small{r^{th}}\) success,

\(~~~~\small{y = number~of~failures~before~r^{th}~success = x-r}\)

We have,\(~~~~~~~~~ \small{P_{nb}(x,p,r)~=~_{x-1}C_{r-1} p^r (1-p)^{x-r} }\)

Substituting from \(\small{y = x-r }\) for \(\small{x}\) in the above expression, we get

\(~~~~~~~~~~\small{P_{nb}(y,p,r)~=~_{y+r-1}C_y p^r (1-p)^y }\)



The probability density functions for a negative binomial distribution for the number of trials \(\small{x}\) required for observing \(\small{r}\) successes and the number of failures \(\small{y}\) before the \(\small{r^{th}}\) success, with \(\small{p}\) being the probability of success in one trial, are summarised below. The mean and variance of these two variables are also given, without derivation:


\(\small{P_{nb}(x,r,p)~=~_{x-1}C_{r-1} p^{r} (1-p)^{x-r},~~~~~~~\mu_x = \dfrac{r}{p},~~~~~~~~~\sigma^2_x = \dfrac{r(1-p)}{p^2} }\)


\(\small{P_{nb}(y,p,r)~=~_{y+r-1}C_y p^r (1-p)^y,~~~~~~~\mu_y = \dfrac{r(1-p)}{P},~~~~~~~~\sigma^2_y = \dfrac{r(1-p)}{p^2} }\)








Why is it called the "negative binomial" distribution?

For any real number \(\small{w}\), the expression \(\small{(1-w)^{-r} }\) with a negative exponent -r can be expanded as a sum using binomial theorem:

\( \small{ (1-w)^{-r}~=~\sum\limits_{x=r}^{\infty} {_{x-1}C_{r-1}} w^{x-r} }\)

The expression for the probability distribution given before is similar to the above negative binomial expansion except for the multiplicative constant \(\small{p^r}\). Hence the name negative binomial distribution .


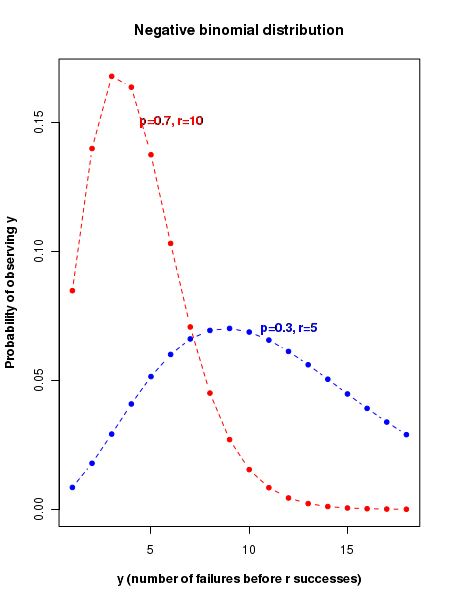
The plot of negative binomial probability distribution

The figure below displays the plots of negative binomial probability distribution for various values of probability \(\small{p}\) of success and the number of failures \(\small{r}\).






Example-1 : The data shows that 9% of child births in India are surgical (cesarean) births. In a random survey, we meet mothers of small children and find out whetehr the child is born by surgical birth. What is the probability that 5th surgical birth is observed when 12 children are born?

If we assign success to finding a child with cesarean birth, this is a negative binomial problem with probability of 12 trials required for 5 successes, with p=0.09 being the probability of success in a trial.

\( \small{P(12~trials~for~5~successes) = _{12-1}C_{5-1} (0.09)^{5} (1-0.09)^{12-5} = _{11}C_{4} (0.09)^{5} (0.91)^{7} = 0.001}\)

Another way of looking at this problem is to consider encountering 12 births for 5 scissarians as 7 non-scissarians before encountering 5 scissarian births. Then, if we take observing scissarian as success and non-scissarian as failure, we can apply second formula with \(\small{y=7}\), \(\small{r=5}\) and \(\small{p=0.09}\) to get,

\( \small{P(observing~7~failures~before~5~successes) = _{y+r-1}C_y p^r (1-p)^y = _{7+5-1}C_7 (0.09)^5 (1-0.09)^7 = 0.001}\)

We will now learn to compute the negative binomial probability distribution in R


R scripts

The usage of these four functions are demonstrated in the R script here. With comments, the script lines are self explanatory: 




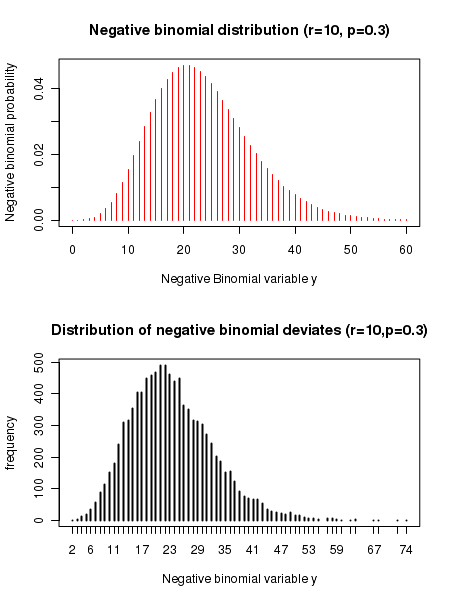
## Negative binomial distribution functions in R

## p = probability of success in a trial
## r = number of successes observed 
## y = number of failures before r successes

## Computing negative binomial probability density for observing y failures before r successes:
y = 5
r = 3
p = 0.3
prob =  dnbinom(y, r, p)

print(paste("Negative binomial probability for " , y , " failures before " , r , " successes is ",prob))


### Function for computing cumulative probability from x=0 to a given value.
### pnbinom(x,r,p) gives cumulative probability for a negative binomial distribution from 0 to x.
x = 5 
cumulative_probability = pnbinom(x,r,p)
print(paste("cumulative negative binomial probability from x=0 to", x," for ", x," failures before ",r, " successes is ", cumulative_probability) )

### Function for finding x value corresponing to a cumulative probability 
cumulative_probability = 0.5
x_value = qnbinom(cumulative_probability, r, p)
print(paste("number of failures corresponding to the given  cumulative binomial probability of ",cumulative_probability," is ",x_value) )

### Function that returns 4 random deviates from a Negative Binomial distribution of given (n,p)
deviates = rnbinom(4, r, p)
print(paste("4 binomial deviates :  "))
print(deviates)


### We plot a binomial density distribution using dnbinom()
r = 10
p = 0.3
y = seq(0,60)
pdens = dnbinom(y,r,p)
plot(y,pdens, type="h", col="red", xlab = "Negative Binomial variable y", ylab="Negative binomial probability", main="Negative binomial distribution (r=10, p=0.3)")

## We generate frequency histogram of binomial deviates using rbinom()
r = 10
p = 0.3
xdev= rnbinom(10000, r, p)
plot(table(xdev), type="h", xlab="Negative binomial variable y", ylab="frequency",main="Distribution of negative binomial random deviates (r=10,p=0.3)")

Executing the above script in R prints the following results and figures of probability distribution on the screen: 



[1] "Negative binomial probability for  5  failures before  3  successes is  0.09529569"
[1] "cumulative negative binomial probability from x=0 to 5  for  5  failures before  3  successes is  0.44822619"
[1] "number of failures corresponding to the given  cumulative binomial probability of  0.5  is  6"
[1] "4 binomial deviates :  "
[1] 6 4 2 5