Biostatistics with R

Theorems on probability

The probability theory can be easily understood using the tools and notations of set theory we studied in our high school. We will quickly recall some fundamental notations of set theory here.

Notations of set theory

Let \(\small{S}\) be a set of all possible events in an experiment.
Let \(\small{A}\),\(\small{B}\), \(\small{C}\),... be the events in the set \(\small{S}\).


We will introduce some symbols to represent the conditional occurances of these events.


Union : \(\small{A \cup B}\) (read as 'A union B') denotes the occurance of at least one of the elements of A or B .

Thus, if A and B are sets of people in a town affected by two diseases 'D1' and 'D2' respectively, \(\small{A \cup B}\) contains the set of people who have either disease D1 or disease D2 .

Accordingly, \(\small{P(A \cup B)}\) denotes the probability of occurance of at least one of the events A or B .

\(\small{P(A \cup B)}\) is also written as \(\small{P(A+B)}\).



Intersection : \(\small{A \cap B}\) (read as 'A intersection B') denotes the occurance of both the events A and B .

Thus, if A and B are sets of people in a town affected by two diseases 'D1' and 'D2' respectively, \(\small{A \cap B}\) contains the set of people who have disease D1 and disease D2 (ie., both the diseases).

Accordingly, \(\small{P(A \cap B)}\) denotes the probability of occurance of both the events A and B .

\(\small{P(A \cap B)}\) is also written as \(\small{P(AB)}\).



Subset : \(\small{A \subset B } \) (read as 'A subset B') denotes that A is a subset of B .

Complement : \(\small{A'} \) represents all elements of S that are not in A . That is \(\small{A' }\) is a complement of set A.

Mutually exclusive event : Events A and B are mutually exclusive if they do not have common elements between them. ie., \(\small{ A \cap B = \phi }\) (null set).
Thus, in a coin throw, Head and Tail are mutually exclusive events.

Mutually exhaustive event : Events A and B are mutually exhaustive if between them they contain all the elements of S. ie., \(\small{A \cap B = S }\)

Formal definition of probability

For each event A in sample space S a positive real number P(A) called probability is assigned such that it satisfies the following properties:

(i) For each event, probability can never exceed 1, and cannot be negative. ie., \(\small{0 \leq P(A) \leq 1 }\)

(ii) Probability of entire sample space is 1, ie., \(\small{P(s) = 1 }\)

(iii) If \(\small{A_1, A_2, A_3, ...,A_k }\) are mutually exclusive events, then
\( \small{ \boxed{ P(A_1 \cup A_2 \cup A_3 \cup .... \cup A_k ) = P(A_1) + P(A_2) + P(A_3) + ....+P(A_k)} }\)

Thus, in a dice throw, \( \small{ P(1~or~2~or~3) = P(1) + P(2) + P(3) = \dfrac{1}{6} + \dfrac{1}{6} + \dfrac{1}{6} = \dfrac{3}{6} } \)


Theorems on probability

There are a few simple theorems on probability we should always remember. We state them below:


Theorem 1 : For each event A in sample space S,    \(\small{ \boxed{P(A) \leq 1}} \)


Theorem 2 : If A and B are events in sample space S and \( A \subset B \), then   \( \small{ \boxed{P(A) \leq P(B)}} \)


Theorem 3 : For each event A in sample space,  \(\small{ \boxed{1 - P(A) = P'(A)} }\)


Theorem 4 : If A and B are two events in sample space S, then,
            \( \small{ \boxed{P(A \cup B) = P(A) + P(B) - P(A \cap B)} } \)


The above formula conect the probability of A or B to occur with the probability of their occurance together. This important formula can be understood in a simple way through Venn diagrams.


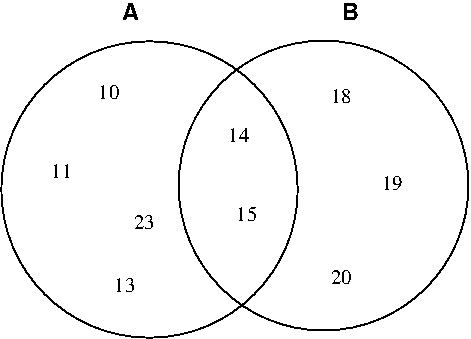
Let   A = {10, 11, 23, 13, 14, 15}   and   B = {14, 15, 18, 19, 20} be two subsets of sample space S. See their Venn diagram below:



We know that to get \(\small{A \cup B }\), we have to merge the elements of A and B avoiding multiple copies of any element. In a set, elements must be unique.

From the above Venn diagram, in order to get \(\small{A \cup B }\), we have to combine the elements in A and B and then subtract the common elements once to avoid double counting.

Thus,     \(\small{A \cup B = \{10,11,23,13,14,15,18,19,20\} }\)     and     \( \small{A \cap B = \{14,15\}} \)


Denoting the number of elements of A, B etc. by the notation n(A), n(B) etc., we write

          \( \small{n(A \cup B) = n(A) + n(B) - n(A \cap B) } \)

Dividing throught by total elements N in sample space S (here N = 9 is elements in sample space), we get,

          \( \small{ \dfrac{n(A \cup B)}{N} = \dfrac{n(A)}{N} + \dfrac{n(B)}{N} - \dfrac{n(A \cap B)}{N} } \)

From the definition of probability of an event as a ratio of the number of favourable elements to the elements in sample space , we realize the the above ratios are corresponding probailities. Therefore we get our relation,

          \( \small{P(A \cup B) = P(A) + P(B) - P(A \cap B) } \)


Example-1 : Three seeds of a rare flower were planted in a garder. Let p(n) represent the probability that n flowers germinate, where n=0,1,2 and 3. Given that \( \small{P(0)=\dfrac{1}{64} }\), \( \small{P(1)=\dfrac{9}{64} }\), \( \small{P(2)=\dfrac{27}{64} }\), find the probabaility \( \small{P(3)}\) that all of them germinate.

Since the sum of all possibilities should be equal to one, we have

\( \small{P(0) + P(1) + P(2) + P(3) = 1} \)

Therefore,     \( \small{ P(3) = 1 - (\dfrac{1}{64} + \dfrac{9}{64} + \dfrac{27}{64}) = \dfrac{27}{64} } \)
Example-2 : A large town had an outbreak of 2 diseases, namely D1 and D2. Medical records showed that 0.3% of population contracted disease D1, 0.21% of population had disease D2 and 0.11% of the population had both the diseases. Compute the probability that a person in the town will suffer from at least one of the diseases.

We know that, \( \small{ D1 \cap D2 }\) represents the condition with both the diseases and \(\small{ D1 \cup D2} \) represents the presence of at least one of them (D1 or D2). Therefore,

\(\small{ P(A \cup B) = P(A) + P(B) - P(A \cap B) = 0.003 + 0.002 - 0.0011 = 0.0039 }\)



R Scripts

R has functions for performing operations on set. We should represent a set as a vector in R.

Thus, if A,B and C are three vectors containing set elements, we can call the union() and intersect() for finding the union and intersection of the sets. These functions can operate on two sets at a time.

In order to form the union and intersection of more than two sets, we need to call these functions successsively.

We can draw a simple Venn diagram of the sets (two or more) by calling the function venn() from the gplots library. See the script below for example calls: 



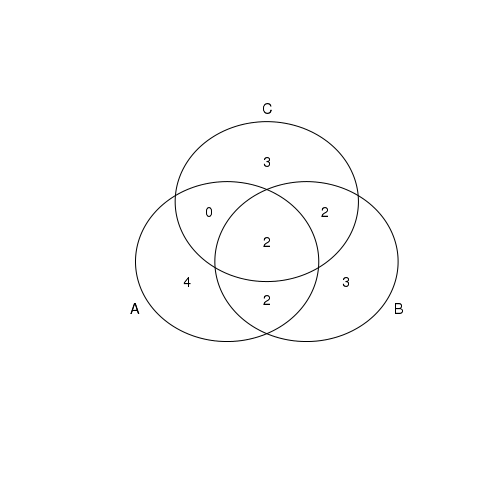
# R functions for set operations

# Define 3 sets with number elements
 A = c(10,20,30,40,50,60,70,80)

 B = c(50,60,70,80,90,100,110,120,130)

 C = c(60,70,100,110,150,170,180)

# Union between sets

 U = union(A,B)

 print("Set A : ")
 print(A)
 cat('\n' )
 

 print("set B : ")
 print(B)
 cat('\n' )
 

 print("set C : ")
 print(C)
 cat('\n' )



 print("union of A and B : ")
 print(U)

 cat('\n')

 # Intersection between the two sets
 I = intersect(A,B)

 print("intersection of A and B : ")
 print(I)

 cat('\n')

 # Union of three sets
 Uthree = union(union(A,B), C)
 
 print("union of A, B and C : ")
 print(Uthree)

 cat('\n')

 # Intersection of three sets. We successively call two at a time.
 Ithree = intersect(intersect(A,B), C)

  print("intersection of A, B and C : ")
  print(Ithree)


 # Venn diagram between the three sets: We use venn() function from gplots.

  library(gplots)
  
  venn(list(A,B,C))

The script prints the following output on the screen, along with a plot shown below. Note that the Venn diagram displays the number of elements in each set and their intersections, and not the acutal elements themselves: 



[1] "Set A : "
[1] 10 20 30 40 50 60 70 80

[1] "set B : "
[1]  50  60  70  80  90 100 110 120 130

[1] "set C : "
[1]  60  70 100 110 150 170 180

[1] "union of A and B : "
 [1]  10  20  30  40  50  60  70  80  90 100 110 120 130

[1] "intersection of A and B : "
[1] 50 60 70 80

[1] "union of A, B and C : "
 [1]  10  20  30  40  50  60  70  80  90 100 110 120 130 150 170 180

[1] "intersection of A, B and C : "
[1] 60 70