Biostatistics with R

Two sample t tests

This test is used to compare the means of two populations which are normally distributed with unknown variances. When the varianes are not known and the sample sizes are large (> 30), we can use a two sample Z test for comparing the means, as explained in the previous section. However, when the sample sizes are small and the variances unknown, we use a t statistic to test the equality of two means.



Let X and Y be two data sets of n and m random samples respectively from normal distributions \(\small{N(\mu_X, \sigma_X)}\) and \(\small{N(\mu_Y, \sigma_Y)}\). Suppose the values of the variances \(\small{\sigma_X^2 }\) and \(\small{\sigma_Y^2 }\) are unknown. Three possibilities arise:

\(~~~~~~~~~~\) (i) The two samples are idependent, population variances are unknown but assumed to be equal.

\(~~~~~~~~~~\) (ii) The two samples are independent, population variances are unknown and unequal.

\(~~~~~~~~~~\) (iii) The two samples are dependent.

These three cases give rise to a family of t-tests which are described below:




1. Two sample t test for independent samples of unknown and equal population variances

We have learnt that, when the variances are unknown and equal, the difference between the means \(\small{\overline{X} }\) and \(\small{\overline{Y} }\) of the two independent samples is known to follow a t disribution of (n+m-2) degrees of freedom with a combined standard deviation \(\small{S_p}\). Computing the standard deviations \(\small{S_X}\) and \(\small{S_Y}\) of the two samples, we write the corresponding T statistic as,

\(\small{ T = \dfrac{\overline{X} - \overline{Y} - (\mu_X - \mu_Y)}{\sqrt{\left[\dfrac{(n-1)S_X^2 + (m-1)S_Y^2}{n-m-2}\right] \left[\dfrac{1}{n} + \dfrac{1}{m}\right] } } ~~ = ~~ \dfrac{\overline{X} - \overline{Y} - (\mu_X - \mu_Y)}{S_p \sqrt{\left[\dfrac{1}{n} + \dfrac{1}{m}\right]}}~~~~~~follows~~~~~t(n+m-1) }\)
where the pooled standard deviation \(\small{S_p}\) is defined as, \(~~~\small{S_p = \sqrt{\dfrac{(n-1)S_X^2 + (m-1)S_Y^2}{n+m-2} } }\)



Using the sample parameters, we construct an approxiamate \(\small{100(1-\alpha)}\) percent confidence interval for \(\small{\mu_X - \mu_Y }\) given by,

\(\small{(\overline{X} - \overline{Y}) \pm t_{1-\frac{\alpha}{2}}(n+m-1) S_p \sqrt{\dfrac{1}{n} + \dfrac{1}{m} } }\)



This t variable can be used as the test statistic for the two sample t test. The null hypothesis can be tested for three possibilities: \(~~~~~~~~\small{\mu_X - \mu_Y = 0,~~~~\mu_X - \mu_Y > 0~~and~~~\mu_X - \mu_Y < 0 }\).

For all the three cases, the hypothesis will be tested at \(\small{\mu_X - \mu_Y = 0}\). Therefore, the t statistic for the test is written as,

\(\small{ T = \dfrac{\overline{X} - \overline{Y}}{\sqrt{\left[\dfrac{(n-1)S_X^2 + (m-1)S_Y^2}{n-m-2}\right] \left[\dfrac{1}{n} + \dfrac{1}{m}\right] } } ~~ = ~~ \dfrac{\overline{X} - \overline{Y}}{S_p \sqrt{\left[\dfrac{1}{n} + \dfrac{1}{m}\right]}}~~~~~~follows~~~~~t(n+m-1) }\)



Under the null hypothesis, this t statistics follows t distribution with (n+m-1) degrees of freedom. We can test a null hypothesis for a given significance level of \(\small{\alpha}\), using the following steps of hypothesis testing.

  • We first compute the sample means \(\small{\overline{X}}\), \(\small{\overline{Y}}\) followed by the sample standard deviations \(\small{s_X}\), \(\small{s_Y}\) from the data.

  • Knowing the value of means and the standard deviations of two data sets, we compute the value of t statistic using the expression given before.

  • The statistical significance (also called "p-value") of this data is then obtained by computing the probability \(\small{P(\gt t) }\) or \(\small{P(\lt -t })\) from the t distribution with (n+m-2) degrees of freedom. Under the null hypothesis, the p-value represents the probability of getting the observed statistic t.

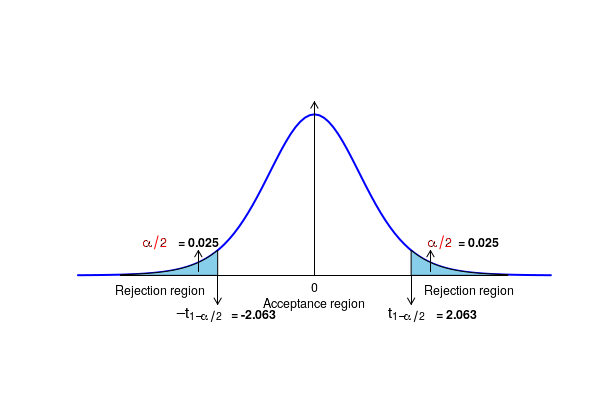
  • If the p-value is either smaller than a pre-decided value \(\small{\alpha}\) or the observed t statistic is outside a given range (\(\small{-t_0 \leq Z \leq t_0) }\), we reject the null hypothesis and accept the alternate hypothesis.

    • Here, \(\small{t_0}\) is the value of statistic above which the area under the t distribution curve for (n+m-2) degrees of freedom is \(\small{\alpha}\).

  • We can also reject the null hypothesis if the computed t statistic for th data is outside the \(\small{(1-\alpha)100\%}\) confidence interval on the population mean.



For the given problem in hand, we set our null hypothesis \(\small{H_0}\)and the alternate hypothesis \(\small{H_1}\) in one of the following three ways:

1. The population mean \(\small{\mu_X}\) is equal to \(\small{\mu_Y}\) . A two sided hypothesis test.
\(~~~~~~~~~~~~~~~~~~~\small{H_0 : \mu_X - \mu_Y = 0,~~or~~\mu_X = \mu_Y} \)
\(~~~~~~~~~~~~~~~~~~~\small{H_A : \mu_X - \mu_Y \neq 0~~or~~\mu_X \neq \mu_Y} \)

The null hypothesis will be rejected in favour of alternate hypothesis for smaller or larger values of t statistic. Accordingly, the rejection region for a given significance level of \(\small{\alpha}\) is given by, \(~~~~\small{t \gt t_{1-\frac{\alpha}{2}}(n+m-2) ~~~~}\) or \(~~~~\small{t \lt -t_{1-\frac{\alpha}{2}}(n+m-2) }\)


2. The population mean \(\small{\mu_X }\) is greater than or equal to \(\small{\mu_Y}\). A one sided hypothesis test.
\(~~~~~~~~~~~~~~~~~~~\small{H_0 : \mu_X - \mu_Y \geq 0~~or~~\mu_X \geq \mu_Y} \)
\(~~~~~~~~~~~~~~~~~~~\small{H_A : \mu_X - \mu_Y \lt 0 ~~ or ~~ \mu_X \lt \mu_Y} \)

The null hypothesis will be rejected in favour of alternative hypothesis for smaller and smaller(ie., more negative) values of t statistic. Accordingly, the rejection region for a given significance level of \(\small{\alpha}\) is given by \(~~~~\small{t \lt -t_{1-\alpha}(n+m-2) }\)

3. The population mean \(\small{\mu_X}\) is less than or equal to \(\small{\mu_Y}\). A one sided hypothesis test.
\(~~~~~~~~~~~~~~~~~~~\small{H_0 : \mu_X - \mu_Y \leq 0~~or~~ \mu_X \leq \mu_Y} \)
\(~~~~~~~~~~~~~~~~~~~\small{H_A : \mu_X - \mu_Y \gt 0~~or~~\mu_X \gt \mu_Y} \)

The null hypothesis will be rejected in favour of alternative hypothesis for larger and larger(positive) values of t statistic. Accordingly, the rejection region for a given significance level of \(\small{\alpha}\) is given by \(~~~~\small{t \gt t_{1-\alpha}(n+m-2) }\)



This test is used in the Example-1 at the end of this tutorial.




3. Two sample t test for independent samples of unknown and unequal population variances - The Welsch t test

We have learnt that When the two population variances are unknown and unequal, the quantity

\(\small{t_w = \dfrac{\overline{X} - \overline{Y} - (\mu_X - \mu_Y)}{\sqrt{\dfrac{S_X^2}{n} + \dfrac{S_Y^2}{m}}} }\) approximately follows a student's t distribution with a modified degrees of freedom \(\small{r}\).

An expression for this modifie degree of freedom is given by the Welch-Satterthwaite correction as,

\(~~~~~~~~~~~~~~~~\small{r = \dfrac{\left(\dfrac{s_X^2}{n} + \dfrac{s_Y^2}{m}\right)^2} {\dfrac{1}{n-1}\left(\dfrac{s_X^2}{n}\right)^2 + \dfrac{1}{m-1} \left(\dfrac{s_Y^2}{m}\right)^2 } }\)



This t variable can be used as the test statistic for the two sample t test. The null hypothesis can be tested for three possibilities: \(~~~~~~~~\small{\mu_X - \mu_Y = 0,~~~~\mu_X - \mu_Y > 0~~and~~~\mu_X - \mu_Y < 0 }\).

For all the three cases, the hypothesis will be tested at \(\small{\mu_X - \mu_Y = 0}\). Therefore, the t statistic for the test is written as,

\(\small{t_w = \dfrac{\overline{X} - \overline{Y}}{\sqrt{\dfrac{S_X^2}{n} + \dfrac{S_Y^2}{m}}}~=~t(r), }\) a student's t distribution with r degrees of freedom.

The \(\small{(1-\alpha)100\%}\) confidence intervl for the difference $\mu_X-\mu_Y$ is given by,

\(~~~~~~~~~~~~~~~~~~~\small{(\overline{X} - \overline{Y}) \pm t_{1-\alpha/2}(r) \sqrt{\dfrac{S_X^2}{n} + \dfrac{S_Y^2}{m} } }\)

Under the null hypothesis, the test statistic follows t distribution with r degrees of freedom. We can test a null hypothesis for a given significance level of \(\small{\alpha}\), using the following steps of hypothesis testing.

  • We first compute the sample means \(\small{\overline{X}}\), \(\small{\overline{Y}}\) followed by the sample standard deviations \(\small{s_X}\), \(\small{s_Y}\) from the data.

  • Knowing the value of means and the standard deviations of two data sets, we compute the value of W which is a t statistic) and the modified degrees of freedom r using the expressions given above.

  • The statistical significance (also called "p-value") of this data is then obtained by computing the probability \(\small{P(\gt W) }\) or \(\small{P(\lt -W })\) from the t distribution with r degrees of freedom. Under the null hypothesis, the p-value represents the probability of getting the observed statistic t.

  • If the p-value is either smaller than a pre-decided value \(\small{\alpha}\) or the observed t statistic is outside a given range (\(\small{-t_0 \leq Z \leq t_0) }\), we reject the null hypothesis and accept the alternate hypothesis.

    • Here, \(\small{t_0}\) is the value of statistic above which the area under the t distribution curve for (n+m-2) degrees of freedom is \(\small{\alpha}\).

  • We can also reject the null hypothesis if the computed t statistic for th data is outside the \(\small{(1-\alpha)100\%}\) confidence interval on the population mean.


The test procedures are same as that of case 1 described before. We will demonstrate this procedure in Example-2 in the problem section at the end of tutorial.




2. Two sample t test for dependent samples (paired t test)

When the two sample sets X and Y are drawn randomly from normal distributions and are dependent, we perform a paired t test for testing the equality of their population means.


In this paired test, the data sets X and Y are not independent, but consist of a set of n paired observtions \(\small{(x_i,y_i) }\), where \(\small{x_i}\) and \(\small{y_i}\) are the measurements on the same sample under two conditions whose effect we want to differentiate in the test. In this case, we do not consider the distribution of the difference in the means \(\small{\overline{X}}\) and \(\small{\overline{Y}}\) but the mean \(\small{\overline{d} }\)of the differences \(\small{d_i = x_i-y_i }\).


Since \(\small{X}\) and \(\small{Y}\) follow Normal distribution, the difference \(\small{d_i = X_i-Y_i }\) must also follow a normal distribution \(\small{N(\mu_d, \sigma_d) }\). Here \(\small{\mu_d,\sigma_d}\) are the mean and standard deviation of population from which the observations \(\small{d_i}\) areassumed to have been randomly drawn.

The population standard deviation of difference \(\small{\mu_d}\) is never known, and we can use the sample standard deviation \(\small{s_d}\) of the differences \(\small{d_i}\) from the data to define a statistic.



The statistic defined by,

\(~~~~~~~~~\small{T = \dfrac{\overline{d} - \mu_d}{\left(\dfrac{S_d}{\sqrt{n}}\right)} ~~~~ }\)

Under the null hypothesis that the population mean difference \(\small{\mu_d=0}\), the variable \(\small{T = \dfrac{\overline{d}}{\left(\dfrac{S_d}{\sqrt{n}}\right)} }\) follows a t distribution with n-1 degrees of freedom



The \(\small{100(1-\alpha) }\) percentage confidence interval for the population mean difference \(\small{\mu_d }\) is given by,

\(\small{ \overline{d}~~\pm~~t_{\alpha/2}(n-1) \dfrac{S_d}{\sqrt{n}} }\)




We use this T variabe for a Hypothesis testing on the population mean difference \(\small{\mu_d}\) of the two variables X and Y. The null and alternate hypothesis can be set up for three following tests:

1. The population mean difference \(\small{\mu_d}\) is zero . A two sided hypothesis test.
\(~~~~~~~~~~~~~~~~~~~\small{H_0 : \mu_d = 0} \)
\(~~~~~~~~~~~~~~~~~~~\small{H_A : \mu_d \neq 0} \)

The null hypothesis will be rejected in favour of alternate hypothesis for smaller or larger values of t statistic. Accordingly, the rejection region for a given significance level of \(\small{\alpha}\) is given by, \(~~~~\small{t \gt t_{1-\frac{\alpha}{2}}(n-1) ~~~~}\) or \(~~~~\small{t \lt -t_{1-\frac{\alpha}{2}}(n-1) }\)


2. The population mean difference \(\small{\mu_d }\) is greater than or equal to zero. A one sided hypothesis test.
\(~~~~~~~~~~~~~~~~~~~\small{H_0 : \mu_d \geq 0} \)
\(~~~~~~~~~~~~~~~~~~~\small{H_A : \mu_d \lt 0 } \)

The null hypothesis will be rejected in favour of alternative hypothesis for smaller and smaller(ie., more negative) values of t statistic. Accordingly, the rejection region for a given significance level of \(\small{\alpha}\) is given by \(~~~~\small{t \lt -t_{1-\alpha}(n-1) }\)

3. The population mean difference \(\small{\mu_d}\) is less than or eual to zero. A one sided hypothesis test.
\(~~~~~~~~~~~~~~~~~~~\small{H_0 : \mu_d \leq 0} \)
\(~~~~~~~~~~~~~~~~~~~\small{H_A : \mu_d \gt 0} \)

The null hypothesis will be rejected in favour of alternative hypothesis for larger and larger(positive) values of t statistic. Accordingly, the rejection region for a given significance level of \(\small{\alpha}\) is given by \(~~~~\small{t \gt t_{1-\alpha}(n-1) }\)



We test a null hypothesis for a given significance level of \(\small{\alpha}\), using the following steps:

  • For each pair of values \(\small{(X_i, Y_i)}\) of the data, we compute their difference \(\small{d_i = X_i-Y_i}\). We then estimate the mean \(\small{\overline{d}}\) and standard deviation \(\small{s_d}\) of these \(\small{d_i}\) values. Let n be the number of pairs of observations.

  • Knowing the value of \(\small{\mu_d, s_d~and~\overline{d}}\), compute the value of T statistic.

  • The statistical significance (also called "p-value") of this data is then obtained by computing the probability \(\small{P(\gt T) }\) or \(\small{P(\lt -T })\) from the t distribution with n-1 degrees of freedom. Under the null hypothesis, the p-value represents the probability of getting the observed t statistic.

  • If the p-value is either smaller than a pre-decided value \(\small{\alpha}\) or the observed T statistic is outside a given range (\(\small{-t_0 \leq Z \leq t_0) }\), we reject the null hypothesis and accept the alternate hypothesis.

    • Here, \(\small{t_0}\) is the value of statistic above which the area under the t distribution curve for (n-1) degrees of freedom is \(\small{\alpha}\).

  • We can also reject the null hypothesis if the computed t statistic for th data is outside the \(\small{(1-\alpha)100\%}\) confidence interval on the population mean.


We will demonstrate this procedure in Example-3 in the problem section at the end of tutorial.


Example-1 : Uknown but equal variances

Milk fat percentage in 2 groups X and Y of Ongole cows of same breed from 2 different farms raised on same feed:

\(\small{X = \{5.23, 5.22, 5.13, 5.56, 5.55, 5.00, 5.17, 5.10, 5.02, 5.48, 4.84, 5.21\} }\)
\(\small{Y = \{4.91, 4.91, 4.64, 5.17, 5.18, 4.75, 5.63, 5.19, 4.56, 5.02, 4.83, 5.59, 4.98, 4.94\} }\)

Assuming that the milk fat percentage in cows follows a normal distribution and the population variances of these two groups to be equal, test whether the mean percentage of milk fat in the two population are significantly different at a level of 0.05.

Since we are testing whether the means are significantly different, the null and the alternate hypothesis are stated as follows:
\(~~~~~~~~~~~\small{H_0 : \mu_X = \mu_Y } \)
\(~~~~~~~~~~~\small{H_A : \mu_X \neq \mu_Y}\)

From the given data sets, we compute the mean and standard deviations:

\(\small{\overline{X}= 5.209,~~~S_X = 0.223,~~~~\overline{Y}=5.021,~~~~S_Y=0.313,~~~~with~~~n=12,~~m=14 }\)

From this, the pooled standard deviation is conmputed:

\(~~~\small{S_p = \sqrt{\dfrac{(n-1)S_X^2 + (m-1)S_Y^2}{n+m-2} } ~=~ \sqrt{\dfrac{(12-1)\times 0.223^2 + (14-1)\times 0.313^2}{12+14-2} }~ = ~ 0.275 }\)

The t statistic is given by,

\(\small{T~~ = ~~ \dfrac{\overline{X} - \overline{Y}}{S_p \sqrt{\left[\dfrac{1}{n} + \dfrac{1}{m}\right]}}~~=~~\dfrac{5.209 -5.021 }{0.275 \times \sqrt{\left[\dfrac{1}{12} + \dfrac{1}{14}\right]}}~~=~~1.738 }\)

Under the null hypothesis that \(\small{\mu_X=\mu_Y }\), this T statitic follows a t-distribution with \(\small{n+m-2 = 12+14-2 = 24}\) degrees of freedom.

Testing null hypothesis using rejection regions

For this two sided test, to a significant level of \(\small{\alpha=0.05 }\), we get, from t-tables, \(t_0 = t_{1-\alpha/2}(n+m-2) = t_{0.975}(24)= 2.063\)

Since the computed value \(\small{T=1.738}\) of the t statistic is within the range (\(\small{-t_0 \leq t \leq t_0) }\), we accept the null hypothesis and reject the alternate hypothesis to a significant level of \(\small{\alpha}\). This acceptance region is marked in the distribution shown below: Testing null hypothesis using p value

The statistical significance of the observed t statistic value of \(\small{T=1.738}\) is given by the area below this value in a t-distribution curve for 24 degrees of freedom. From the R function call "qt(1.738, 24)", we compute this p-value to be \(\small{0.0475}\). Since this computed p value of the data is higher than the two sided significance \(\small{\alpha/2=0.025}\), we accept the null hypothesis to a significant level of 0.05.

Testing null hypothesis using confidence interval

We can also reject the null hypothesis if the computed t statistic for the data is outside the confidence interval on the population mean. An approxiamate \(\small{100(1-\alpha)}\) percent confidence interval for \(\small{\mu_X - \mu_Y }\) given by,

\(\small{(\overline{X} - \overline{Y}) \pm t_{1-\frac{\alpha}{2}}(n+m-2) S_p \sqrt{\dfrac{1}{n} + \dfrac{1}{m} } }\)



We have computed values from the data:

\(\small{n=12,~~~m=14,~~~~\overline{X} = 5.209,~~~ \overline{Y}=5.021,~~~~~t_{1-\frac{\alpha}{2}}(n+m-2) = t_{0.975}(24) = 2.0639,~~~}\)
\(\small{S_p = 0.275,~~~~~\alpha = 0.05 }\)

Substituting these values into the above expression for the two sided \(\small{95\% }\)confidence interval, we get the confidence interval to be \(\small{0.188 \pm 0.223 }\). Since this confidence interval contains the null hypothesis value 0 for the difference in the mean of X and Y data set, we accept the null hypothesis that the two population means are equal.

Example-2 : Unknown and unequal variances - Welsch test

Milk fat percentage in Sahiwal and Ongole breeds (denoted as X and Y respectively) from the same farm are given below:

\(\small{ X = \{4.95, 5.37, 4.70, 4.96, 4.72, 5.17, 5.28, 5.12, 5.26, 5.48\} }\)
\(\small{ Y = \{4.65, 4.86, 4.57, 4.56, 4.96, 4.63, 5.04, 4.92, 5.37, 4.58, 4.26, 4.40\} }\)

Assuming that the milk fat percentage in cows follows a normal distribution, test whether the mean percentage of milk fat in the two population are significantly different at a level of 0.05.


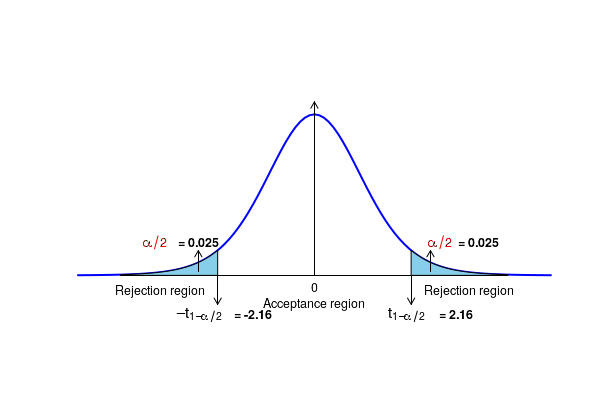
Since there is no information on the equality of the varinces of the two populations, we take them to be unequal and perform a Welsch t test for testing the equality of means. We will test the null hypothesis that the population means of milk percentagein for both breeds are equal. $H_0 : \mu_X = \mu_Y$.



From the given data sets, we compute the mean and standard deviations:

\(\small{\overline{X}=5.101 ,~~~S_X = 0.264,~~~~\overline{Y}= 4.733 ,~~~~S_Y= 0.307 ,~~~~with~~~n=10,~~m=12 }\)

The statistic for the Welsch t test is computed as,

\(\small{t_w = \dfrac{\overline{X} - \overline{Y}}{\sqrt{\dfrac{S_X^2}{n} + \dfrac{S_Y^2}{m}}}~~=~~= \dfrac{5.101 - 4.733 }{\sqrt{\dfrac{0.264^2}{10} + \dfrac{0.307^2}{12}}}~~=~~3.02 }\)

The modified degrees of freeson r is computed using the Welsch-Satterthwaite correction formula as,

\(~~~~\small{r = \dfrac{\left(\dfrac{s_X^2}{n} + \dfrac{s_Y^2}{m}\right)^2} {\dfrac{1}{n-1}\left(\dfrac{s_X^2}{n}\right)^2 + \dfrac{1}{m-1} \left(\dfrac{s_Y^2}{m}\right)^2}~~=~~\dfrac{\left(\dfrac{0.264^2}{10} + \dfrac{0.307^2}{10}\right)^2} {\dfrac{1}{10-1}\left(\dfrac{0.264^2}{10}\right)^2 + \dfrac{1}{12-1} \left(\dfrac{0.307^2}{12}\right)^2}~~=~~19.96 }\)

We approximately take the degrees of freedom to the nearest integer to be $r=20$.

Under the null hypotesis, the statistic $t_w$ follows t distribution with $r=20$ degrees of freedom.

Testing null hypothesis using p value

Since the null hypothesis $H_0 : \mu_X = \mu_Y$ can be rejected by higher and lower values of the distribution, this is a two sided test. With $\alpha=0.05$, we take $\alpha/2 = 0.025$ to be the significnce level on each side for testing the hypothesis.

We compute the probability of getting a t statistic value above $t_w = 3.04$ in a t distribution with 24 degrees of freedom. From either t table or R function call "1 - pt(3.04, 20)" this is comuted to be 0.00323. Since this probability is less than the significance level 0.025, we reject the two sided null hypothesis to a significance level of 0.05.

Testing null hypothesis using rejection regions

For this two sided test, to a significant level of \(\small{\alpha=0.05 }\), we get, from t-tables, \(t_0 = t_{1-\alpha/2}(r) = t_{0.975}(20)= 2.086\)

Since the computed value \(\small{t_w=3.02}\) of the t statistic is outside the range (\(\small{-t_0 \leq t \leq t_0) }\), we reject the null hypothesis and accept the alternate hypothesis to a significant level of \(\small{\alpha}\).

Confidence interval for the difference in population means

A $95\%$ confidence interval for the observed difference between population means is,

\(\small{(\overline{X} - \overline{Y}) \pm t_{1-\alpha/2}(r) \sqrt{\dfrac{S_X^2}{n} + \dfrac{S_Y^2}{m} } ~=~(5.101 - 4.733) \pm 2.086 \sqrt{\dfrac{0.264^2}{10} + \dfrac{0.307^2}{12} } ~=~(0.114, 0.622) }\)
Example-3 : Two sample t test for dependent variables (paired t test)

A trial was conducted to test the effect of a routine health check up procedure on the pulse rate of healthy adults. For 14 adults, their pulse rate in units of bpm were measured before and after the procedure. The resuts are given beow:

Individual :\(\small{~~~~~~~~~~~~~~~~~1~~~~~~~2~~~~~~~3~~~~~~~4~~~~~~~5~~~~~~~6~~~~~~~7~~~~~~8~~~~~~~9~~~~~~~10~~~~~~11~~~~~~12~~~~~~13~~~~~~~14}\)

Before procedure :\(\small{~~~95~~~~106~~~~79~~~~~71~~~~90~~~~~79~~~~71~~~~77~~~~103~~~~103~~~~92~~~~~~63~~~~~~82~~~~~~76}\)

After procedure : \(\small{~~~~97~~~~~116~~~~82~~~~81~~~~82~~~~86~~~~107~~~~86~~~~94~~~~~~91~~~~~~85~~~~~~98~~~~~~91~~~~~~87 }\)

Assuming the pulse rate of adults follow Gaussian, test whether the pulse rates have changed significantly after the procedure.


Since have a paired data sets drawn from normal distribution, we will perform a dependent t test for comparing their population means.

In the following table, we compute the difference $d_i$ between the pairs of data points to compute the mean $\overline{d}$ and the standard deviation $S_d$:

Individual $X_i$ $Y_i$ $d_i = X_i-Y_i$ $d_i - \overline{d}$ $(d_i - \overline{d})^2$
1 95 97 -2 4.86 23.59
2 106 116 -10 -3.14 9.88
3 79 82 -3 3.86 14.88
4 71 81 -10 -3.14 9.88
5 90 82 8 14.86 220.73
6 79 86 -7 -0.14 0.02
7 71 107 -36 -29.14 849.31
8 77 86 -9 -2.14 4.59
9 103 94 9 15.86 251.45
10 103 91 12 18.86 355.59
11 92 85 7 13.86 192.02
12 63 98 -35 -28.14 792.02
13 82 91 -9 -2.14 4.59
14 76 87 -11 -4.14 17.16

\(\small{~~~~~~~~~~~~~~~~~~~~~~~Sum :~~ -96~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~2745.71}\)

mean \(\small{\overline{d} = \dfrac{-96}{14} = -6.85 }\)
Standard deviation = \(\small{S_d = \dfrac{\sqrt{2745.71}}{14-1} = 14.53 }\)

The t statistic : \(~~~~~~~~~\small{T = \dfrac{\overline{d}}{\left(\dfrac{S_d}{\sqrt{n}}\right )}~=~ \dfrac{-6.85}{\left(\dfrac{14.53}{\sqrt{14}}\right)} = -1.76 }\)

Testing null hypothesis using the rejection region:

For a significance level of \(\small{\alpha=0.05}\), the critical value for the null hypothesis is computed as,

\(\small{-t_{1-\alpha/2}(n-1) = -t_{0.975}(13) = -2.16 }\)

Since out t-statistic value from data is negative (ie., -1.76), we take the negative criticl value. Accordingly,the acceptance and rejection regions for the null test are marked in the figure below: Since the t-statistic value of -1.76 from the data is to the right of critical value -2.16 on the negative side, it is in the acceptance region. Hence we accept the null hypothesis to state that the pulse rates have not changed significantly after the prcedure.

Testing null hypothesis using the p-value:

The computed T statistic follows t(n-1), a t-distribution with n-1 degrees of freedom. From the t table or by using the R function call "pt(-1.76, 13)", we get the p value to be 0.0509. Since this is greater than the two sided probability of 0.025 for hypothesis testing, we accept the null hypothesis to state that the pulse rates have not changed significantly after the procedure.

R-scripts

in R, the family of student's t-tets can be performed with a single call to the function t.test(). We can perform one sample and two sample tests. The function call with all the essential parameters is described below: 


       t.test(x, y, alternative, mu, paired, var.equal, conf.level) 

where

       x, y  = data vectors of two observations

       alternative  = A character string specifying alternate hypothesis.

			    alternate can take three values :  "two.sided", "less", "greater"

		               It can also be a vector with all the above three strings, in which
		               case all the three hypothesis will be tested.

                                "less" means the population mean of x is less than that of y.
				"greater" mens the population mean of x is greater thn that of y. 

			        default value is  "two.sided" 


 
       mu  = a number indicating the true value of the mean for one smple test, and

                the difference in the means in the case of two sample test.

       paired   = A logical value of TRUE or FALSE  indicating whether it is a paired or unpaired test.

          Default is  FALSE   and hence an unpaired t test
                     

     conf.level = confidence level of the interval. 
                   For example,  conf.level=0.95  sets a 95% confidence interval.



The function returns a vector with two numbers :  (p value, Z statistics) .


       two_sample_Z_test(x, y, sigma_x, sigma_y, alpha, null) 

where

       x, y  = data vectors of two observations

       sigma_x, sigma_y  = population standard deviations
 
       alpha  = significane level

       null   = string value indicating type of null hypothesis.
      
  Possible values of variable null are:   "equal", "less_than_or_equal", "more_than_or_equal" 

The function returns a data structure from which the p-value of the test and the confidence interval can be
extracted along with other input values. 


Imortant Note : The p-value for a two sided test is the sum of p-values on bothe sides. it is alpha value.

See the R code example below for various tests with this function.








## R script using t.test() library function for various t tests

##-------------------------  Test-1 --------------------------------------------

### Two sample t-test between two independent variables with unequal population variances
###  This is "Welsch t-test"

##we set a confidence level of 0.95

# data sets
Xvar=c(4.95,5.37,4.70,4.96,4.72,5.17,5.28,5.12,5.26,5.48)

Yvar=c(4.65,4.86,4.57,4.56,4.96,4.63,5.04,4.92,5.37,4.58,4.26,4.40)

## The test is for a null hypothesis of equality of means. Alternate says that the means are unequal. Hence this is a two sided alternatie hypothesis.
## The difference between two population means is zero.  

## call to the t.test() function
res = t.test(x=Xvar, y=Yvar, alternative="two.sided", var.equal=FALSE, paired=FALSE, conf.level=0.95)

## Print the result summary
print(res)


## Note : To perform a two smple independent t test with equality of variance, set "var.equal=TRUE" in the above function call


print("------------------------------------------")



##-----------------------------  Test-2 -----------------------------------------

## Two sample t-test with dependent variables (paired t-test) 

data_before = c(95,106,79,71,90,79,71,77,103,103,92,63,82,76)

data_after = c(97,116,82,81,82,86,107,86,94,91,85,98,91,87)

## we test the null hypothesis that the population means of 2 variables are equal
##  to a significance level of 0.95

## call to the t.test() function
res = t.test(x=data_before, y=data_after, alternative="two.sided", paired=TRUE, conf.level=0.95)

print(res)
## 






Executing the script in R prints the following lnes of test results:




	Welch Two Sample t-test

data:  Xvar and Yvar
t = 3.0216, df = 19.966, p-value = 0.006749
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 0.1138185 0.6215148
sample estimates:
mean of x mean of y 
 5.101000  4.733333 

[1] "------------------------------------------"

	Paired t-test

data:  data_before and data_after
t = -1.7654, df = 13, p-value = 0.101
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -15.248261   1.533975
sample estimates:
mean of the differences 
              -6.857143