Biostatistics with R

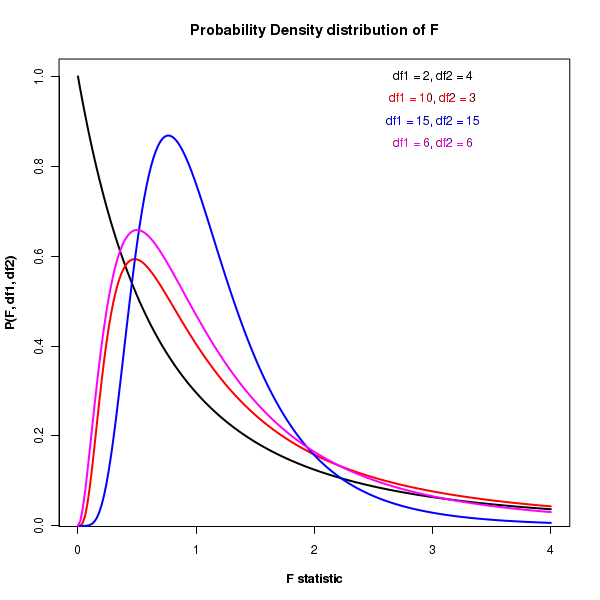
The F distribution

The F distribution arises when we compare the variances of two normal distributions by taking their ratio.

Suppose we draw random samples of sizes \(\small{n_1}\) and \(\small{n_2}\) from two normal distributions \(\small{N(\mu_1, \sigma_1^2) }\) and \(\small{N(\mu_2, \sigma_2^2) }\) respectively. Let \(\small{s_1^2 }\) and \(\small{s_2^2 }\) be the estimated variances of these two data sets.

We are interested in the ratio of \(\small{\dfrac{\sigma_1^2}{s_1^2} }\) over \(\small{\dfrac{\sigma_2^2}{s_2^2} }\). We write their ratio as,

\(\small{F = \dfrac{ \left(\dfrac{s_1^2}{\sigma_1^2}\right) } { \left(\dfrac{s_2^2}{\sigma_2^2}\right) } = \dfrac { \dfrac{\left[ \dfrac{(n_1-1)s_1^2 } {\sigma_1^2 } \right]}{(n_1-1)} } { \dfrac{\left[ \dfrac{(n_2-1)s_2^2 } {\sigma_2^2 } \right]}{(n_2-1)} } = \dfrac{U/r_1}{V/r_2} ~~~~~ }\)where we have defined the new variables as,

\(\small{U = \dfrac{(n_1-1)s_1^2}{\sigma_1^2} ~~~}\), \(\small{V = \dfrac{(n_2-1)s_2^2}{\sigma_2^2}~~~ }\), \(\small{r_1 = (n_1-1)~~ }\) and \(\small{~~r_2 = (n_2-1) }\).















The variables U and V are known to be chi-square variables with \(\small{r_1}\) and \(\small{r_2}\) degrees of freedom respectively. The ration given by \(\small{F = \dfrac{U/r_1}{V/r_2}}\) is shown to follow a continuous distribution called F distribution with two variables \(\small{ r_1 = n_1-1 }\) and \(\small{ r_2 = n_2-1}\) that represent two degrees of freedom . Thus, for each pair of values \(\small{(r_1,r_2)}\), we have a separate F distribution written as \(\small{F(r_1,r_2)}\).

The expression for the probability density function for a given value \(\small{F=w }\) on a F distribution with degrees of freedom \(\small{(r_1,r_2) }\) is given by,

\(\small{P_F(w,r_1,r_2) = \dfrac{ \left(\dfrac{r_1}{r_2}\right)^{(r_1/2 )} \Gamma\left[\dfrac{r_1+r_2}{2}\right] w^{r_1/2 - 1 }} {\Gamma(\dfrac{r_1}{2}) \Gamma(\dfrac{r_2}{2}) \left[ 1 + \left(\dfrac{r_1w}{r_2}\right)^{(r_1 + r_2)/2} \right] } }\)









The plots of the PDF distribution of F is shown below for few pairs of \(\small{(r_1,r_2) }\) values:





Computation of probabilities from F distribution

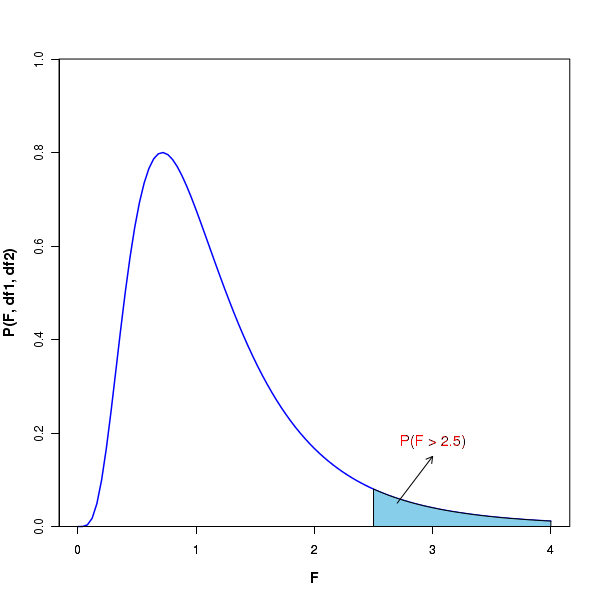
Similar to what we did with the Gaussian distribution, we can compute the probability of getting more than or less than certain value of F statistic.See the figure below:





In the above figure, the plot at the top shows the shaded area which represent the probabilities above a particular \(\small{F}\) value.

In an F distribution with given degrees of freedom df1 and df2, there is a p-value corresponding to every F value that represents the area under the curve above that F. Because of this complexity, separate tables are generally prepared for a discrete set of p-values. From each table, given a set of df1 and df2 values, we can get the F value above which the area under the curve is p.

One such F-distribution table can be accessed from here. In this table, the \(\small{F}\) values corresponding to \(\small{\alpha = 0.1, 0.05, 0.025, 0.01, 0.001}\) are tabulated for many pairs of degrees of freedom (df1, df2) for certain discrete values in the range of 1 to 120.

Look at the the table corrsponding to p=0.05, for example. Corresponding to a degrees of freedom \(\small{df1=n-1=10}\) and \(\small{df2=n-2=10 }\), the p-value of 0.05 represents the area undet the F curve above F=2.9782.

Similarly, let us look at the table corresponding to p=0.01. For the degrees of freedom \(\small{ df1=12}\) and \(\small{df2 = 15 }\), the p-value of 0.01 represents the area under the curve above F=2.10485.

We can write the above statements as,

\(~~~~~~~~~~~~~\small{F_{0.05}(df1=10, df2=10) = 2.9782} \)

and, \(~~~~~\small{F_{0.01}(df1=12, df2=15) = 2.10485} \)

To get a p-value for any value of F statistic from the distribution F(df1, df2), R provides a function \(~~\small{pf(F, df1, df2)}\) which returns the area under the F diatribution from \(\small{F = 0~to~t}\) for given degrees of freedom \(\small{df1, df2}\). This is illustrated in the R scripts below.



Now we will learn to use the R library functions for the t distribution.



R scripts 



Let     F  = F distribution varible

        n  = sample size

        r1 = n1-1,   r2 = n2-1  = degrees of freedom


Then,


  df(F, r1, r2)  -----> returns the probability density at t on a F distribution curve with degrees of freedom r1, r2.
  
  rf(m, r1, r2)  -----> returns m random deviates from r distribution with r1 and r2 degrees of freedom            

  qf(p, r1, r2)  -----> returns the F value corresponding to a cumulative probability p on a F distribtuion with r1 and f2 degrees of freedom. 
       
  pf(F, r1, r2)  -----> returns the cumulative probability p from minus infinity to F on a F distribution with r1 and r2 degrees of freedom.





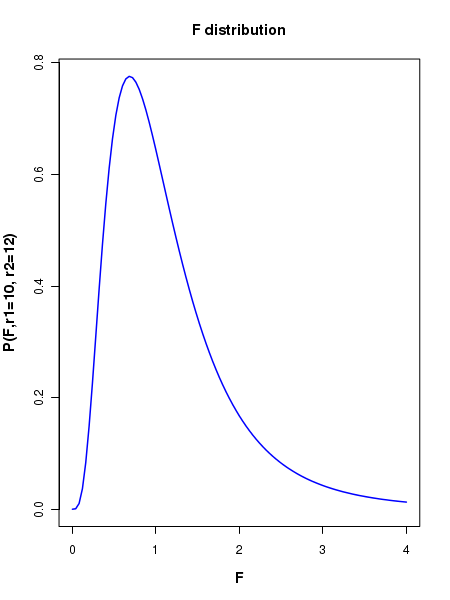
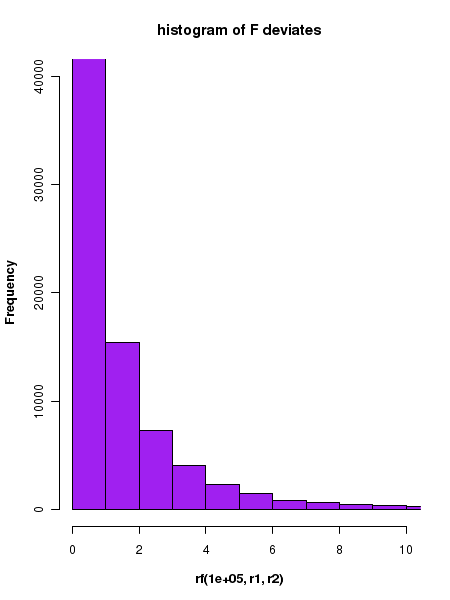
##### Using R library functions for the F distribution

#### probability density function
n1 = 10
n2 = 12
r1 = n1-1
r2 = n2-2
F = 2.5

F_density = df(F, r1, r2)
F_density = round(F_density, digits=2)
print(paste("probability density for F = ", F, " and degree of freedom = ", r1," and ", r2, " is ", F_density))

### Generating the curve of F distribution probability density

x = seq(0,5,0.1)

r1 = 10
r2 = 12

string = "P(F,r1=10, r2=12)"

curve(df(x, r1, r2), xlim=c(0,4), xlab="F", ylab=string, lwd=1.5, cex.lab=1.2, col="blue", main="F distribution", font.lab=2)


#### Generating cumulative probability (p-value) above upto a F value in a F distribution

#######  pf(F, r1, r2) generates cumulative probability from 0 to given F value.
#######  The probability of having a value above F is 1 - pf(F, r1, r2)

r1 = 10
r2 = 12

F = 2.8
pvalue = pf(F, r1, r2)
pvalue = round(pvalue,3)
print(paste("cumulative probability from F = 0 to ", F, "is ", pvalue))


#### Generating F value for which the cumulative probability from 0 to F is p.
###  The function qf(p,r1, r2) returns F value at which cumulative probability is p.

p = 0.95  ## cumulative probabilitu from 0 to F.
F = qf(p, r1, r2)
F = round(F, digits=3)
print(paste("F value for a cumulative probability p = ", p, "is ", F))


#### Generating random deviates from a t distribution
### rf(m, f1, f2) returns a vector of m random deviates from a F of given F(r1,r2)

r1 = 10
r2 = 12
ndev = rf(4, r1, r2)
ndev = round(ndev,digits=3)
print("Four random deviates from F distribution with (10, 12) degrees of freedom : ")
print(ndev)

X11()

## plotting the histogram of 100000 random deviates from unit Gaussian:
r1 = 10
r2 = 12
hist(rf(100000, r1, r2), breaks=60, xlim = c(0,10), ylim = c(0, 40000), col="purple", main="histogram of F deviates")

Executing the above script in R prints the following results and figures of probability distribution on the screen: 


[1] "probability density for F =  2.5  and degree of freedom =  9  and  10  is  0.09"
[1] "cumulative probability from F = 0 to  2.8 is  0.953"
[1] "F value for a cumulative probability p =  0.95 is  2.753"
[1] "Four random deviates from F distribution with (10, 12) degrees of freedom : "
[1] 1.157 0.169 0.787 1.044