CountBio
Mathematical tools for natural sciences
Basic Statistics with R
Confidence interval for the population variance
In an earlier section, while sampling from a normal distribution, we learnt to construct a confidence interval for a population mean based on the sample mean.
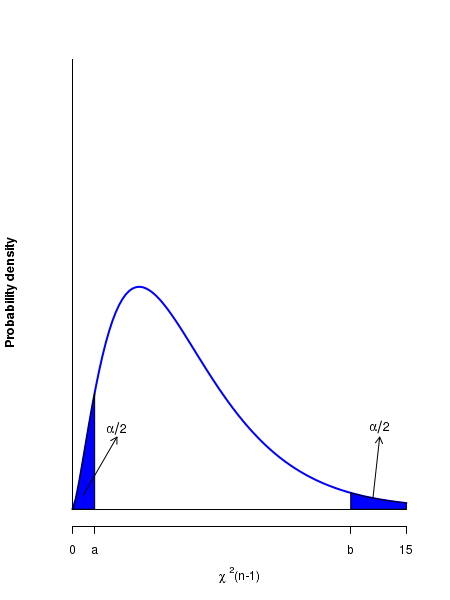
Once the sample set X of size n is measured and sample mean \(\small{\overline{x}}\) is computed, we can construct an interval \(\small{\overline{x} \pm Z_{1-\alpha/2}\left(\dfrac{\sigma}{\sqrt{n}}\right)}\) around this mean. We can say with \(\small{(1-\alpha)\times 100\% }\) confidance that the unknown population mean \(\small{\mu }\) is in this interval, provided we know the population standard deviation \(\small{\sigma }\).Arguing on similar lines, a \(\small{100(1-\alpha)\%}\) confidence interval for the population variance \(\small{\sigma^2 }\) can be defined around the sample variance \(\small{s^2 }\) based on n data points from a normal distribution. The sample variance is computed from the n data points using, $$ \small{ s^2 = \dfrac{1}{n-1}\sum_{i=1}^n (x_i - \overline{x})^2 } $$ From the properties of the Chi-square distribution, we know that the variable defined as \(\small{\dfrac{(n-1)s^2}{\sigma^2} }\) follows \(\small{\chi^2(n-1) }\), a Chi-square distribution with (n-1) degrees of freedom. On a Chi-square distribution with (n-1) degrees of freedom, we choose two points \(\small{a}\) and \(\small{b }\) for the Chi-square variable such that the area under the curve(probability of observing a $\chi^2$ value) between these two points is \(\small{1-\alpha}\). (ie., the area from 0 to \(\small{b}\) is \(\small{1-\alpha/2 }\) and the area from 0 to \(\small{a}\) is \(\small{\alpha/2 }\). The area in the two tail regions are equal to \(\small{\alpha/2 }\). Thus the area under \(\small{\chi^2(n-1)}\) curve between points \(\small{a}\) and \(\small{b}\) is \(\small{1-\alpha }~~\). See the figure below
We can therefore write,
\(~~~~~~~~~~\small{1~-~\alpha~~=~~P\left( a~\leq~\dfrac{(n-1)s^2}{\sigma^2}~\leq~b \right) }\)
\(~~~~~~~~~~~~~~~~~~~~~~\small{=~P\left(\dfrac{a}{(n-1)s^2}~\leq~\dfrac{1}{\sigma^2}~\leq~\dfrac{b}{(n-1)s^2} \right) }\)
\(~~~~~~~~~~~~~~~~~~~~~~\small{=~P\left(\dfrac{(n-1)s^2}{b}~\leq~\sigma^2~\leq~\dfrac{(n-1)s^2}{a} \right) }\)
Thus the probability that the random interval \(\small{\left[\dfrac{(n-1)s^2}{b},~\dfrac{(n-1)s^2}{a} \right]}\) contains the unknown parent vairance \(\small{\sigma^2}\) is \(\small{1-\alpha}\)