analysis of variance, one way anova

Biostatistics with R

One Factor Analysis of Variance (One way ANOVA)

In One factor Analysis Of Variance, we compare three or more treatment data sets. Suppose there are m data sets to compare. These m data sets are assumed to have been randomly drawn from m normal distributions of unknown means $\small{\mu_1, \mu_2, \mu_3, ......,\mu_m }$ and unknown but common variance $\small{\sigma^2 }$.

We wish to test the equality of means of the m normal distributions. The null hypothesis is written as,

$\small{~~~~~~~~~~~~~~~~~~~~~H_0~:~\mu_1~=\mu_2~=\mu_3~=......=~\mu_m~=\mu }$.

We test the above null hyptheis of equality of means against all possible alternate hypothesis. Note that $\small{\mu }$ is not known here.

We use the index i, with $\small{i=1,2,3,4,.....m }$ to represent a data set $\small{X_i}$ of size $\small{n_i}$ randomly drawn from a normal distribution $\small{N(\mu_i, \sigma^2) }$.

The individual elements of the data set $\small{X_i}$ are written with a double index $\small{X_{ij}}$as follows:

$~~~~~~~~~~~~~~~~~~~~~~~~~~\small{X_1~=~\{X_{11}, X_{12}, X_{13},.......,X_{1n_1}\} }~~~~~~~$ first data set with $n_1$ observations

$~~~~~~~~~~~~~~~~~~~~~~~~~~\small{X_2~=~\{X_{21}, X_{22}, X_{23},.......,X_{1n_2}\} }~~~~~~~$ second data set with $n_2$ observations
$~~~~~~~~~~~~~~~~~~~~~~~~~~\small{.}$
$~~~~~~~~~~~~~~~~~~~~~~~~~~\small{.}$
$~~~~~~~~~~~~~~~~~~~~~~~~~~\small{.}$
$~~~~~~~~~~~~~~~~~~~~~~~~~~\small{X_i~=~\{X_{i1}, X_{i2}, X_{i3},.......,X_{in_i}\} }~~~~~~~$ data set i with $n_i$ observations
$~~~~~~~~~~~~~~~~~~~~~~~~~~\small{.}$
$~~~~~~~~~~~~~~~~~~~~~~~~~~\small{.}$
$~~~~~~~~~~~~~~~~~~~~~~~~~~\small{.}$
$~~~~~~~~~~~~~~~~~~~~~~~~~~\small{X_m~=~\{X_{m1}, X_{m2}, X_{m3},.......,X_{mn_m}\} }~~~~~~~$ last data set m with $n_m$ observations.

Here, $~~~\small{i=1,2,3,....,m }~~~~~~$denotes individual data sets and $~~~~~\small{j=1,2,3,.....,n_i }~~~$ denotes elements of a data set i

Let $~~n~=~n_1+n_2+n_3+....+n_m~~$ be the total number of observations in all data sets.

We proceed with the analysis in steps:

$~~~~~~~~~~$ Step 1 : Compute the mean of individual data sets and the whole data

The mean of a data set i is computed as,

$~~~~~~~~~~~~\small{\overline{X}_{i\large\cdot}~=~\dfrac{1}{n_i}\displaystyle{\sum_{j=1}^{n_i}X_{ij}}~~=~~\dfrac{X_1+X_2+X_3+.....+X_{n_i}}{n_i} }$

where the dot in the symbol $\overline{X}_{i\large\cdot}$ indicates that for a given data set i, the summation over elements j have been carried out. Hence we replace j by dot symbol.

The mean of the whole data set is computed by summing all the data sets and dividing by the total number of data points in all of them together:

$\small{\overline{X}_{\large{\cdot \cdot}}~=~\dfrac{1}{n}\displaystyle{\sum_{i=1}^{n}\sum_{j=1}^{m}X_{ij}}~=~\dfrac{(X_{11}+X_{12}+....+X_{1n_1})+(X_{21}+X_{22}+....+X_{2n_2}) + .....+ (X_{m1}+X_{m2}+....+X_{mn_m}) }{n} }$

where the double dot in the symbol $\small{\overline{X}_{\large{\cdot \cdot }} }$ indicated that the summation has been carried out over both the indices i and j. Hence a double dot (one dot for i and one for j).

The above computations are summarized in the following table:

-------------------------------------------------------------------------------------------------------------------
data set $~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~$data points$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~$mean values
-------------------------------------------------------------------------------------------------------------------
$~~X_1 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~X_{11}, X_{12}, X_{13},........X_{1n_1}~~~~~~~~~~~~~~~~~~~\overline{X}_{1\large\cdot} $

$~~X_2 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~X_{21}, X_{22}, X_{23},........X_{2n_2}~~~~~~~~~~~~~~~~~~~\overline{X}_{2\large\cdot} $

$~~X_3 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~X_{31}, X_{32}, X_{33},........X_{3n_3}~~~~~~~~~~~~~~~~~~~\overline{X}_{3\large\cdot} $
$~~\large\cdot~~~~~~~~~~~~~~~~~~~~~~~~~~~~\large\cdot~~~~~~~~\large\cdot~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\large\cdot $
$~~\large\cdot~~~~~~~~~~~~~~~~~~~~~~~~~~~~\large\cdot~~~~~~~~\large\cdot~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\large\cdot $
$~~\large\cdot~~~~~~~~~~~~~~~~~~~~~~~~~~~~\large\cdot~~~~~~~~\large\cdot~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\large\cdot $
$~~\large\cdot~~~~~~~~~~~~~~~~~~~~~~~~~~~~\large\cdot~~~~~~~~\large\cdot~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\large\cdot $
$~~X_m ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~X_{m1}, X_{m2}, X_{m3},........X_{mn_m}~~~~~~~~~~~~~~~~\overline{X}_{m\large\cdot} $

$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~Grand~mean~~=~~\overline{X}_{\large{\cdot\cdot}}$

--------------------------------------------------------------------------------------------------------------------

$~~~~~~~~~~$ Step 2 : Partition the variance of the whole data set into components

The variance associated with the whole data is obtained by sum squares of deviation of each data point $X_{ij}$ from the grant mean $\overline{X}_{ij}$. The sum square term ("the total sum square (SST)") is written as,

$\small{~~~~~~~~~~~~~SST~=~\displaystyle{\sum_{i=1}^{m}\sum_{j=1}^{n_j}(X_{ij}-\overline{X}_{\large\cdot\cdot})^2} }$

The aim here is to write the above total sum of squares into two parts - the sum of squares within data sets and the sum squares among the data sets. In order to achive this, we add and substract the term $\small{\overline{X}_{i\large\cdot}}$ to the total sum square expression and manipulate the summation terms:

$\small{~~~~~~~~~~~~~SST~=~\displaystyle{\sum_{i=1}^{m}\sum_{j=1}^{n_i}(X_{ij}-\overline{X}_{\large\cdot\cdot})^2} }$

$\small{~~~~~~~~~~~~~~~~~~~~~~~~~~~~=~\displaystyle{\sum_{i=1}^{m}\sum_{j=1}^{n_j}(X_{ij}-\overline{X}_{i\large\cdot} + \overline{X}_{i\large\cdot} - \overline{X}_{\large\cdot\cdot})^2} }$

$\small{~~~~~~~~~~~~~~~~~~~~~~~~~~~=~ \displaystyle{\sum_{i=1}^{m}\sum_{j=1}^{n_i}(X_{ij}-\overline{X}_{i\large\cdot})^2} + \displaystyle{\sum_{i=1}^{m}\sum_{j=1}^{n_i}(\overline{X}_{i\large\cdot}-\overline{X}_{\large\cdot \large\cdot})^2} + 2 \displaystyle{\sum_{i=1}^{m}\sum_{j=1}^{n_i}(X_{ij} - \overline{X}_{i\large\cdot}) ( \overline{X}_{i\large\cdot}-\overline{X}_{\large\cdot \large\cdot}) } }$

In the second sum, since there is no j index inside, summing the term for j from 1 to $n_i$ is same as multiplying the term by $n_i$:

$\small{ \displaystyle{\sum_{i=1}^{m}\sum_{j=1}^{n_i}(\overline{X}_{i\large\cdot}-\overline{X}_{\large\cdot \large\cdot})^2}~=~ \displaystyle{\sum_{i=1}^{m} n_i(\overline{X}_{i\large\cdot} - \overline{X}_{\large\cdot\cdot})^2 } }$

The summation in the third term evaluates to zero, as shown below:

$\small{2 \displaystyle{\sum_{i=1}^{m}\sum_{j=1}^{n_i}(X_{ij} - \overline{X}_{i\large\cdot}) ( \overline{X}_{i\large\cdot}-\overline{X}_{\large\cdot \large\cdot}) }= 2 \displaystyle{\sum_{i=1}^{m}\left[(\overline{X}_{i\large\cdot} - \overline{X}_{\large\cdot\cdot}) \sum_{j=1}^{n_i} (X_{ij} - \overline{X}_{i\large\cdot})\right] } ~=~ 2 \displaystyle{\sum_{i=1}^{m}(\overline{X}_{i\large\cdot} - \overline{X}_{\large\cdot\cdot}) (n_i \overline{X}_{i\large\cdot} - n_i \overline{X}_{i\large\cdot} )~=~0 } }$

Incorporating these results into the expression for SST,

$\small{SST~=~\displaystyle{ \sum_{i=1}^{m}\sum_{j=1}^{n_j}(X_{ij}-\overline{X}_{\large\cdot\cdot})^2~=~\sum_{i=1}^{m}\sum_{j=1}^{n_i}(X_{ij}-\overline{X}_{i\large\cdot})^2 ~+~\sum_{i=1}^{m}n_i(\overline{X}_{i\large\cdot}-\overline{X}_{\large\cdot \large\cdot})^2 } }$

$\small{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~SST~~~~~~~~~=~~~~~~~~~~~~SSW~~~~~~~~~~~~~~+~~~~~~~~~~~SSA }$

The three terms SST, SSW and SSA are understood as follows:

$\small{SST~=~\displaystyle{ \sum_{i=1}^{m}\sum_{j=1}^{n_j}(X_{ij}-\overline{X}_{\large\cdot\cdot})^2} ~~~~~~~}$ is the total sum of squares. It is the measure of variance in the $~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~$whole data.

$\small{SSW~=~\displaystyle{ \sum_{i=1}^{m}\sum_{j=1}^{n_j}(X_{ij}-\overline{X}_{i\large\cdot})^2} ~~~~~~~}$is the sum of squares within a treatment. Called error sum of squares

$\small{SSA~=~\displaystyle{ \sum_{i=1}^{m}n_i(X_{i\large\cdot}-\overline{X}_{\large\cdot\cdot})^2} ~~~~~~~}$is the sum of squares among treatments . Called between treatment $~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~$ sum of squares

The total variance of the whole data set is thus resolved into variance within data sets and variance among data sets. Using these terms, a statistic will be derived which follows a probability distribution under null hypothesis.

$~~~~~~~~~~$ Step 2 : Expression for a statistic in terms of observed sums of squares

Under the null hypothesis $H_0:\mu_1=\mu_2=\mu_3=.....=\mu_m$, the quantities $\small{SST/(m-1)}$ and $\small{SSE/(n-m)}$ both are unbiased estimators of $\sigma^2$. Also, $\small{SST/\sigma^2 }$ and $\small{SSE/\sigma^2 }$ both are independent chi-square variables

Therefore, under the null hypothesis $H_0:\mu_1=\mu_2=\mu_3=.....=\mu_m$, the ratio

$\small{\dfrac{SST/(m-1)}{SSW/(n-m)}~=~\dfrac{\left[SST/\sigma^2\right]/(m-1)} { \left[SSW/\sigma^2\right]/(n-m) }~=F~~~}$ is a F distribution with (m-1) and (n-1) degrees of freedom.

When the population means are equal, the total sumof squares SST is small and hence F is small. When the population means are unequal, the value of SST is relatively large and hence the value of F gets larger and the null hypothesis $H_0$ is rejected for very large values of F.

For a given value of $\alpha$, the critical region will be $~~F \geq F_\alpha(m-1, n-m)$

$~~~~~~~~~~$ Simplified formulae for the observed sums of squares

The following simplified expressions can be used for computing SST and SSA to make the calculations easier:

$\small{SST~=~\displaystyle{ \sum_{i=1}^{m}\sum_{j=1}^{n_i}X_{ij}^2~-~\dfrac{1}{n}\left[\sum_{i=1}^{m}\sum_{j=1}^{n_i}X_{ij}\right]^2 } ~~~~~~~}$

$\small{SSA~=~ \displaystyle{ \sum_{i=1}^{m} \dfrac{1}{n_i}\left[\sum_{j=1}^{n_i}X_{ij}\right]^2~-~\dfrac{1}{n}\left[\sum_{i=1}^{m}\sum_{j=1}^{n_i}X_{ij}\right]^2 } }$

and

$~~~~~~~~~~~~~~~~~~~~~\small{SSW~=~SST~-~SSA}$

For computaional purposes, the meaning of each term in the above formula is as follows:

$\small{ \displaystyle{ \sum_{i=1}^{m}\sum_{j=1}^{n_i}X_{ij}^2 } }~~$means $~~$ "square every number in every data set and add all of them"

$\small{\displaystyle{\left[\sum_{i=1}^{m}\sum_{j=1}^{n_i}X_{ij}\right]^2 }}~$ means$~$ "sum all the numbers across all the data sets (grand total) and square it".

$\small{\displaystyle{ \sum_{i=1}^{m} \dfrac{1}{n_i}\left[\sum_{j=1}^{n_i}X_{ij}\right]^2 }}~~$ means $~$ "sum all numbers in a data set and square the sum. Divide this sum square by the number of data points in the data set. Do this for all the data sets and add the results".

Example-1 :

The cholesterol level of four groups of adults with distince food habits among the groups were compared in an experiment. The results are present below:

$Group-1~:~~220~~214~~203~~184~~186~~200~~165$
$Group-2~:~~262~~193~~225~~200~~164~~266~~179$
$Group-3~:~~272~~192~~190~~208~~231~~235~~141$
$Group-4~:~~190~~255~~247~~278~~230~~269~~289$

Assuming that these four data sets follow Normal distributions $N(\mu_i, \sigma)$, test the null hypothesis that $\mu_1=\mu_2=\mu_3=\mu_4$ to a significance level of 0.05.

Since the four populations are assumed to be Gaussian with equal standard deviations, we will perform one way ANOVA to test the equality of their populations means.

For the convenience of symbols, let us denote the four data sets as $X_1, X_2, X_3$ and $X_4$. We write the ANOVA table to perfor the computation as follows:

---------------------------------------------------------------------------------------------------------------------
$Variable~~~~~~~~~~~~~~~~~~~~~Observations~~~~~~~~~~~~~~~~~~~~~~~~~~~\displaystyle\sum_{j=1}^{7}X_{ij}~~~~~~~~~~~~~~\displaystyle\sum_{j=1}^{7}X_{ij}^2$
---------------------------------------------------------------------------------------------------------------------
$~~~X_1~~~~~~~~~~~~220~~214~~203~~184~~186~~200~~165~~~~~~~~~~~~~1372~~~~~~~~~~~~~~~~271082$

$~~~X_2~~~~~~~~~~~~262~~193~~225~~200~~164~~266~~179~~~~~~~~~~~~~1489~~~~~~~~~~~~~~~~326211$

$~~~X_3~~~~~~~~~~~~272~~192~~190~~208~~231~~235~~141~~~~~~~~~~~~~1469~~~~~~~~~~~~~~~~318679$

$~~~X_4~~~~~~~~~~~~190~~255~~247~~278~~230~~269~~289~~~~~~~~~~~~~1758~~~~~~~~~~~~~~~~448200$

-----------------------------------------------------------------------------------------------------------------------
$~~~~~~~~~~~~~~~~~~~~Totals~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~6088~~~~~~~~~~~~~~~1364172$
-----------------------------------------------------------------------------------------------------------------------

We identify various terms in the F stistic:

$ \displaystyle{ \sum_{i=1}^{m}\sum_{j=1}^{n_i}X_{ij}^2}~=~1364172 $

$\displaystyle{\dfrac{1}{n}\left[\sum_{i=1}^{m}\sum_{j=1}^{n_i}X_{ij}\right]^2}~=~\displaystyle{\dfrac{1}{28} \left[6088\right]^2}~=~1323705$

$\displaystyle{ \sum_{i=1}^{m} \dfrac{1}{n_i}\left[\sum_{j=1}^{n_i}X_{ij}\right]^2 ~~=~~\dfrac{1}{7}\left[1372\right]^2 + \dfrac{1}{7}\left[1489\right]^2 + \dfrac{1}{7}\left[1469\right]^2 + \dfrac{1}{7}\left[1758\right]^2}~=~ 1335433$

$~~~~~SST~=~1364172-1323705~=~40467$

$~~~~~SSA~=~1335433-1323705~=~11728$

$~~~~~SSW~=~SST~-~SSA~~=~~40467-11728~=~28739$

$~~~~~F~=~\displaystyle{\dfrac{SST/(m-1)}{SSW/(n-m)}~=~\dfrac{40467/(4-1)}{28739/(28-4))}}~=~11.26~~$is the computed F statistic.

Using the R function call for F distribution,

$F_{0.05}(4,28)~=~qf(0.95,3,24)~=~3.01$

The critical region for rejection of null hypothesis is $~~F \ge 3.01$.

Since the computed value $F=11.26$ is outside the critical region, the null hypothesis $H_0 : \mu_1=\mu_2=\mu_3=\mu_4$ is rejected to a sinificant level of 0.05. We accept the alternate hypothesis to state that the four population means are not equal.

R has many functions to perform one way anova, as shown below:

R scripts


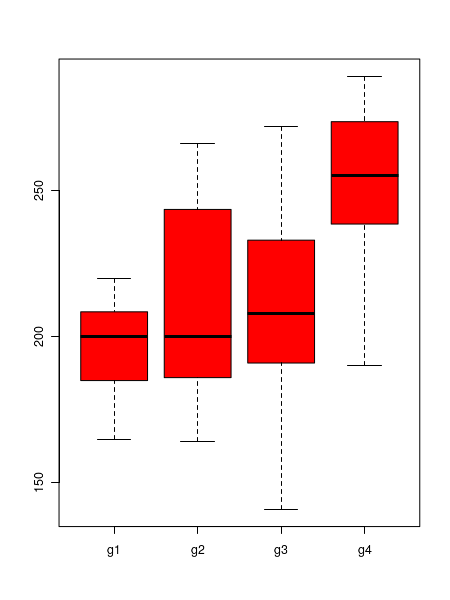
In R, two functions namely aov() and oneway.test()
perform one way anova. They have a very specific inut data structure in the form of a 2 column data frame with category and values of data. 

First step is to create the input file from data. Te second step is to run call the functions in R script.

For example, consider the cholesterol level data among four groups Group-1, Group-2, Group-3 
and Group-4 presented in Example-1. We show it below:

Group−1 :  220  214  203  184  186  200  165
Group−2 :  262  193  225  200  164  266  179
Group−3 :  272  192  190  208  231  235  141
Group−4 :  190  255  247  278  230  269  289

We shorten the names to G1, G2, g3 and G4. 

These 4 setscan be written as a two column data in which first column is the value against 
which the group label is given. See below:

(two colums can be tb separated(*.txt file) or comman separated (*.csv file)

value  group
220     g1
214     g1
203     g1
184     g1
186     g1
200     g1
165     g1
262     g2
193     g2
225     g2
200     g2
164     g2
266     g2
179     g2
272     g3
192     g3
190     g3
208     g3
231     g3
235     g3
141     g3
190     g4
255     g4
247     g4
278     g4
230     g4
269     g4
289     g4

The above data format is stored as a text file with a txt extension. 
We give some name like, "cholesterol_anova_data.txt". 
It can also be stored as a comma separated csv format.

This has the advantage that we can handle data sets of different lengths. 
If you store it as data frame, then many NA's may be required to make them equaal length. 
Above format is better.

Once this file "anova_data.txt" is ready, we can write an R script 
for performing one factor ANOVA as follows:


##analysis of oneway anova in R

## read data into a frame called "dat"
dat = read.table("cholesterol_anova_data.txt", header=TRUE)

## compute and print the mean values of groups
print( mean(dat$value[dat$group=="g1"]) )
print( mean(dat$value[dat$group=="g2"]) )
print( mean(dat$value[dat$group=="g3"]) )
print( mean(dat$value[dat$group=="g4"]) )

## box plot to compare the data sets
boxplot(dat$value ~ dat$group, col="red")

# one way anova test. Default assumption is variances not equal.
oneway.test(dat$value~dat$group)

# To make variences equal, set parameter
oneway.test(dat$value~dat$group, var.equal=TRUE)

# Run anov function
aov.out = aov(count ~ spray, data=InsectSprays)
summary(aov.out)


(i) In the above script, the call boxplot(dat$value ~ dat$group, col="red") creates the following plot:

   
   
    
  

We can clearly see that there is a substantial difference of means within the four data sets.





(ii) The function call  oneway.test(dat$value~dat$group)  with the assumption that the variances are equal (default assumption) to print the following results:


	One-way analysis of means (not assuming equal variances)

data:  dat$value and dat$group
F = 4.3553, num df = 3.000, denom df = 12.568, p-value = 0.02577

For a F statisti value of 4.355 with 3 degrees of freedom, the p-value for the test is 0.02577. If we set an \(\small{\alpha=0.05}\), this rejects the null hypothesis that the mean cholesterol levels for the 4 groups are equal




(iii) The function call  oneway.test(dat$value~dat$group, var.equal=TRUE)  performs the test with the assumptions of unequal variances among four distributions and prints similar results:


	One-way analysis of means

data:  dat$value and dat$group
F = 3.2646, num df = 3, denom df = 24, p-value = 0.03884


(iii) The function call aov.out = aov(count ~ spray, data=InsectSprays) and its summary print the following information:




	    Df Sum Sq Mean Sq F value Pr(> F)    
spray        5   2669   533.8    34.7 > 2e-16 ***
Residuals   66   1015    15.4                   
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1


In this case, the statistical significance is extremenly small.

CountBio

Mathematical tools for natural sciences

Biostatistics with R

One Factor Analysis of Variance (One way ANOVA)

R scripts