CountBio

Covariance and Correlation

Consider two random variables X and Y that take numerical values. What kind of relationship can exist between X and Y?

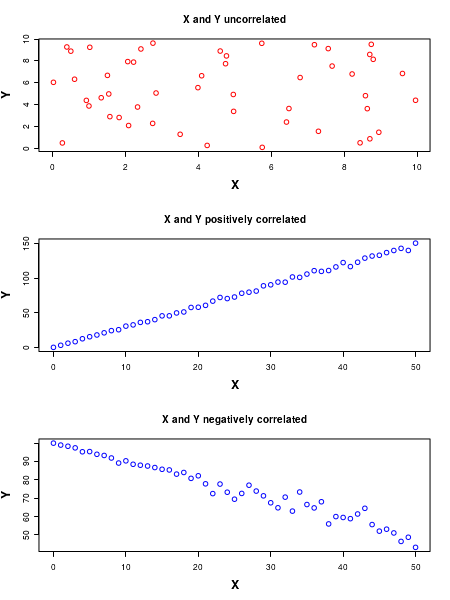
There are three possibilities:

1. There is no relatonship between X and Y. ie., they are independent of each other.

2. When X increases, Y also increases. The two vriables are said to be positively correlated

3. When X increases, Y decreases.The two variables are said to be negatively correlated

See the figure below:

Covariance

Covariance is a measure that detects whether two variables vary together or independent of each other.

If X and Y are two data sets with size n and sample means \(\small{\overline{x}}\) and \(\small{\overline{y}}\) respectively, then the covariance of X and Y is defined as,

\(\small{Cov(X,Y)~=\dfrac{1}{n-1} \sum\limits_{i=0}^n (x_i-\overline{x})(y_i-\overline{y}) }\)

Cov(X,Y) is close to zero when X and Y are independent variables (uncorrelated).

Cov(X,Y) is positive when Y increases as X increases (positive correlation).

Cov(X,Y) is negative when Y decreases as X increases (negative correlation).










Suppose X and Y are independent variables. Then the sign of \(\small{x_i-\overline{x}}\) is independent of the sign of \(\small{y_i-\overline{y}}\) and their product has equal chance of taking negative or positive sign. Therefore their summation is a small number close to zero.

Assume that when X increases, Y also increases. Then for most of the data points, \(\small{x_i-\overline{x}}\) and \(\small{y_i-\overline{y}}\) take the same sign (ie., \(\small{x_i}\) is below \(\small{\overline{x}}\) when \(\small{y_i}\) is below \(\small{\overline{y}}\). Similarly, \(\small{x_i}\) is above \(\small{\overline{x}}\) when \(\small{y_i}\) is above \(\small{\overline{y}}\)), making their product a large positive number.

Assume that when X increases, Y decreases. Then for most of the data points, \(\small{x_i-\overline{x}}\) and \(\small{y_i-\overline{y}}\) take opposite signs (ie., \(\small{x_i}\) is above \(\small{\overline{x}}\) when \(\small{y_i}\) is below \(\small{\overline{y}}\). Similarly, \(\small{x_i}\) is below \(\small{\overline{x}}\) when \(\small{y_i}\) is above \(\small{\overline{y}}\)), making their product a large negative number.

Correlation coefficient

The covariance Cov(X,Y) described above is not normalized. The positive and negative values taken by Cov(X,Y) can be very large or small depending on the unit chosen for X and Y.

In order to tackle this problem, a term called correlaton coefficient is defined to normalize X and Y to their standard deviations, thus making the quantity a dimensionless number between -1 to +1 through zero.

There are may definitions of correlation coefficient. The Preason's Correlation Coefficient is widely used as a measure of correlation. Let \(\small{\overline{x}}\), \(\small{\overline{y}}\) and \(\small{s_x}\), \(\small{s_y}\) be the mean and standard deviations of the two samples X and Y respectively for a sample size n. Then, the Peasrson's correlation coefficient is defined as,

\(\small{R_{xy}~=\dfrac{1}{n-1} \sum\limits_{i=0}^n \left(\dfrac{x_i-\overline{x}}{s_x}\right)\left(\dfrac{y_i-\overline{y}}{s_y}\right) }\)

\(\small{R_{xy} = 0}\) when X and Y are uncorrelated).

\(\small{R_{xy} = 1}\) when X and Y have perfectly positive correlation.

\(\small{R_{xy} = -1}\) when X and Y have perfectly negative correlation.

If correlation between X and Y is not perfect, then a non-zero positive number between 0 and 1 indicates positive correltion and

\(\small{ 0 \lt R_{xy} \lt 1}\) is the region of positive correlation.

\(\small{ -1 \lt R_{xy} \lt 0}\) is the region of negative correlation.

R-scripts

In R, the functions, cov() computes the covariance between two data sets.

Similarly, the function cor() computes the Pearson'r correlation coefficient between two data sets

Both the function are defined with similar arguments as,

       cov(x,y)  returns the covariance.

       cor(x,y)returns Pearson'r correlation coefficient

where


       x  = a vector of data set X
 
       y  = a vector of data set Y

     
Thse two functions are used in the R script below      

##################################################
## Compute the covariance and correltion for the following dataset:

x = c(10,20,30,40,50,60,70,80,90,100)

y = c(95, 220, 279, 424, 499, 540, 720, 880, 950, 1200)

cv = cov(x,y)

cr = cor(x,y)

print(paste("covarince = ", round(cv, digits=3)))

print(paste("Pearsons correlection coefficient = ", round(cr, digits=3)))

##############------------------------------------------------

Executing the above script in R prints the following results and figures of probability distribution on the screen:

[1] "covarince =  10549.444"
[1] "Pearsons correlection coefficient =  0.988"