CountBio

Plotting a mathematical function

Given an expression for a function y(x), we can plot the values of y for various values of x in a given range. This can be accomplished using an R library function called curve().

Plotting a simple function directly

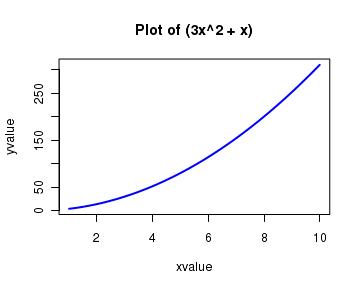
We now plot s simple function $ y = 3x^2 + x $ in the range $x = [1,10]$ as follows:

curve(  3*x^2 + x, from=1, to=10, n=300, xlab="xvalue", ylab="yvalue", 
             col="blue", lwd=2, main="Plot of (3x^2 + x)"  )

The above command gives the following plot:

The important parameters of the function curve() used in this call are as follows:

     An  mathematical expression as a first parameter. The expression is written using the 
     format for writing mathematical operations in R 

     Two number parameters called  from  and  to  that represent the first and 
      the last points of the range of independent parameter x.

      n  is an integer that represents the number of points (values of x) equally 
      spaced between  from  and  to  values. The values of the function are
      computed at these  n  points.

      The other parameters like  xlab, ylab, col, lwd, main  have their usual meaning
       as in the plot() function.

To plot an equation

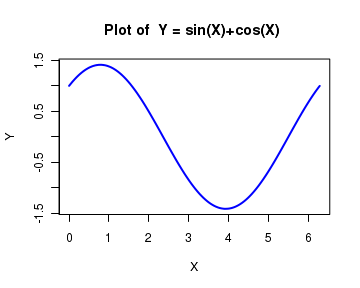
An equation defined outside the curve() can be passed as a parameter to it. We have to define an external R function implementing the equation and pass it as a parameter to curve(). In the following function call, we define an external R function called "eqn" that returns the value of the expression $sin(x)+cos(x)$ for a given x. We then pass it to the function curve() for plotting it. We plot this equation in the range $[0, 2\pi]$ at 200 equally spaced values of x in between:

eqn = function(x){sin(x)+cos(x)}

curve(eqn, from=0, to=2*pi, n=200, xlab="Y", ylab="X", col="blue",lwd=2, 
             main="Plot of  Y = sin(X)+cos(X) ")

Adding a new plot to the existing plot

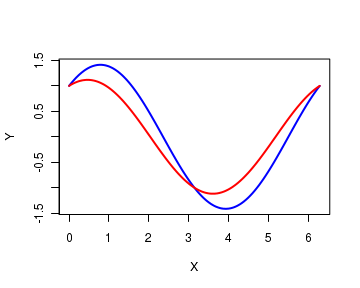
More than one function can be plotted in the same graph by using a parameter add, which takes boolean values TRUE or FALSE. When add=TRUE, the current curve will be added to the existing curve.

In the following script, we define two equations and plot them on the same plot. The first formula is plotted as before, and the second one is plotted using the parameter value add=TRUE in the function call:

equation1 = function(x){sin(x)+cos(x)}

curve(equation1, from=0, to=2*pi, n=300, xlab="X", ylab="Y", col="blue",lwd=2, 
             main="Plot of  Y = sin(X)+cos(X) ")

equation2 = function(x){0.5*sin(x)+cos(x)}

curve(equation2, from=0, to=2*pi, n=300, add=TRUE, xlab="X", ylab="Y", col="red",lwd=2, 
             main="Plot of  Y = sin(X)+cos(X) ")

Curve with logarithmic scale

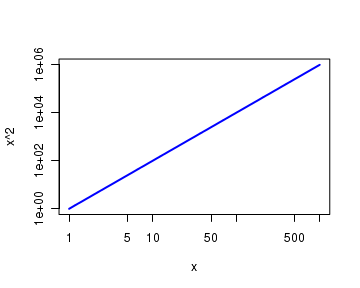
Similar to the plot() function, the parameter log sets the logarithmic scale (natural logarithm). log="xy" sets both the axes to log scale. Similarly, log="x" and log="y" set the X and Y axis respectively to the log scale. See the example below where we plot a function $y = x^2$ in the range [1,100] in logarithmic scale for both the axes.

curve( x^2, from=1, to=1000, log = "xy", col="blue", lwd=2 )